오차역전파법
경사하강법으로 손실함수의 최솟값을 찾으려는 방법을 이전 장에서 알아봤습니다. 오차역전파법은 오차를 역으로 전파하는 방법으로 가중치 매개변수의 기울기를 효율적으로 계산하는 방법입니다. 오차역전파법을 위한 도구로 연쇄 법칙을 알아보고, 신경망에서의 오차역전파 전체를 한 번 보겠습니다.
1. 연쇄 법칙 Chain rule
오차역전파법을 이해하기 위해서는 기본적으로 연쇄 법칙에 대해 이해해야합니다.
연쇄 법칙은 합성함수의 미분을 각 함수의 미분의 곱으로 나타내는 것입니다.

위 식과 같은 합성함수 z가 있을 때 미분은 다음과 같이 나타낼 수 있습니다.

우변의 t가 지워져 좌변과 같아지는 것을 알 수 있습니다. 여기서 우변의 두 분수는 z를 t로 미분한 것과 t를 x로 미분한 것입니다. 이것은 x -> t -> z의 과정을 거치는 함수를 거슬러(z -> t -> x) 올라가며 이전(역전파 순서) 층의 값을 현재 층의 변수로 미분해준 것들을 곱한 것과 같습니다.
따라서, 연쇄 법칙은 합성함수를 거슬러 올라가는 단계에서의 국소적 미분들을 곱하는 것이라고 볼 수 있습니다.

2. 역전파
연쇄 법칙에서 합성함수를 "거슬러 올라간다"라는 표현을 사용하였습니다. 거꾸로 거슬러 올라가며 각 국소적 미분들을 곱하여 역으로 전파하는 이것을 역전파라고 합니다.
1) 덧셈의 역전파
z = x + y라는 단순 덧셈 함수를 각각의 변수로 미분해주면 다음과 같습니다.

따라서 연쇄법칙으로 미분을 한다면 다음과 같습니다.

덧셈의 과정을 거슬러 올라갈 때 국소적 미분이 1이 나오기 때문에 연쇄법칙 진행되어도 1이 곱해져 미분식이 바뀌지 않습니다.
2) 곱셈의 역전파
z = xy라는 단순 곱셈 함수를 각각의 변수로 미분해주면 다음과 같습니다.

따라서 연쇄법칙으로 미분을 한다면 다음과 같습니다.

곱셈의 역전파는 순전파 때의 입력신호들을 "서로 바꾼 값"을 곱하는 것과 같습니다.
3) 나눗셈의 역전파
y = 1/x라는 식을 미분하면 다음과 같습니다.

따라서 역전파의 과정에서 나눗셈이 나올 경우 이전(역전파 순서) 층의 변수를 제곱하고 마이너스를 붙힌 값을 곱해주게 됩니다.
3. 활성화 함수 역전파
앞 절에서 살펴본 사칙연산(- 는 +에 포함)들의 역전파를 사용해 활성화 함수들의 역전파를 하나하나 살펴보겠습니다.
(1) ReLu 함수 역전파

ReLu함수를 미분하면 다음과 같습니다.

따라서 이를 연쇄법칙을 통해 역전파한다면 다음과 같습니다.

순전파 때 입력값이 0 초과면 역전파에서 그대로, 입력값이 0이하였으면 역전파 때 0으로 계산됩니다.
(2) Sigmoid 함수 역전파
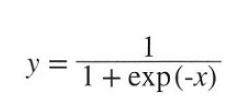
시그모이드 함수의 과정을 나타내면 다음과 같습니다.
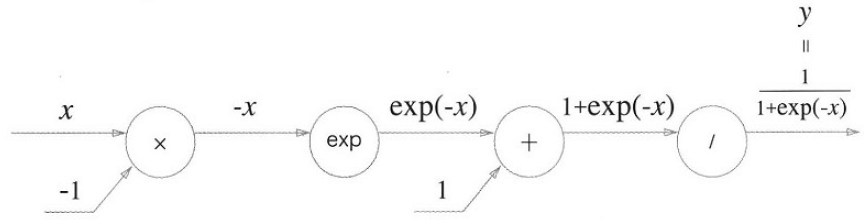
중간에 상숫값들이 들어오는게 마치 편향이 추가된 신경망을 보는 듯 합니다. 각 단계별로 역전파를 통해 미분을 곱해간다면 다음과 같습니다.

지수함수의 경우 미분을 할 경우 자신 그대로 이기 때문에, 이전(역전파 순서) 층에 출력된 지수함수값을 그대로 곱해주는 과정을 더합니다. 이 과정들을 단순화해서 나타낸다면 다음과 같습니다.
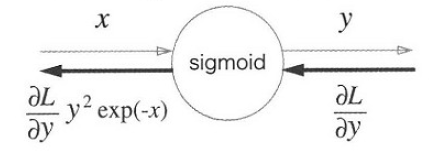
또 역전파의 결과값을 다음과 같이 정리할 수 있습니다.
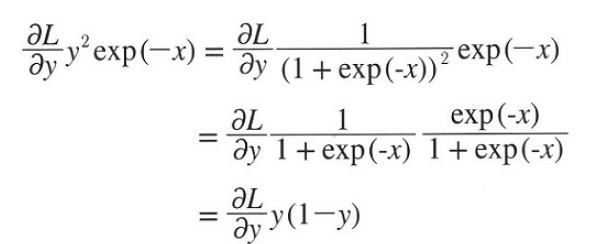
따라서, Sigmoid함수의 역전파는 순전파의 출력 즉 y만으로 계산할 수 있습니다.
4. Affine/Softmax 함수
1) Affine 변환
Affine 변환이란 신경망의 순전파 때 수행되는 행렬곱을 기하학에서 말하는 것입니다.
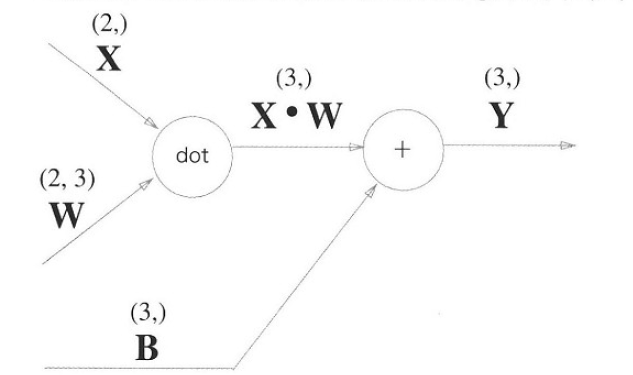
모든 입력값을 X라는 행렬에, 모든 가중치값을 W에 포함시켰을 때 Affine변환은 위 그림과 같이 표현할 수 있고, 이의 역전파는 다음과 같습니다.
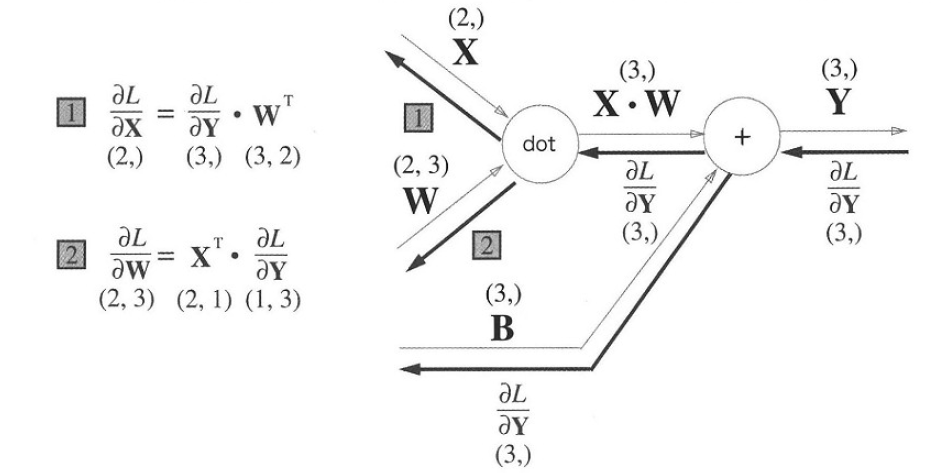
행렬들이 전치되는 과정은 선형대수를 공부했다면 알 수 있습니다. 여기서는 다차원 배열간의 곱셈에서 차원 수를 맞춰주기 위해 전치되었다고만 이해하고 넘어가도 좋습니다.
배치용 Affine변환에서는 입력값의 행 그리고 그 행차원으로 이뤄지는 미분식이 배치의 크기 N을 따른 다는 것을 생각하면 다음 그림의 이해가 쉽습니다.
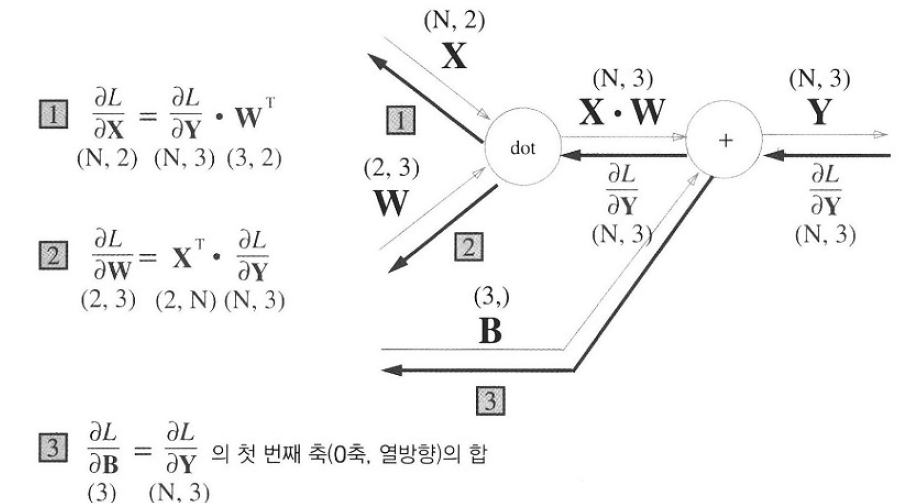
2) Softmax-with-Loss
소프트맥스 함수는 입력 값을 정규화 하여 출력합니다. 예시는 다음과 같습니다.
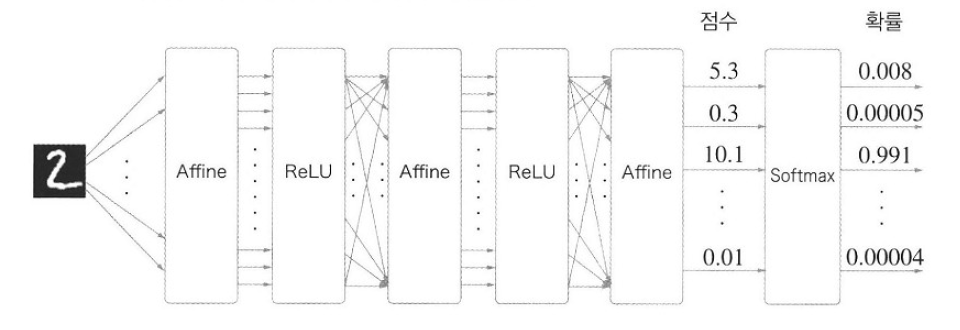
Softmax함수를 출력층의 활성화함수로 사용하고, 손실함수로 교차 엔트로파 오차를 사용했을 경우 손실함수에서부터의 오차역전파를 그림으로 나타내면 다음과 같습니다.
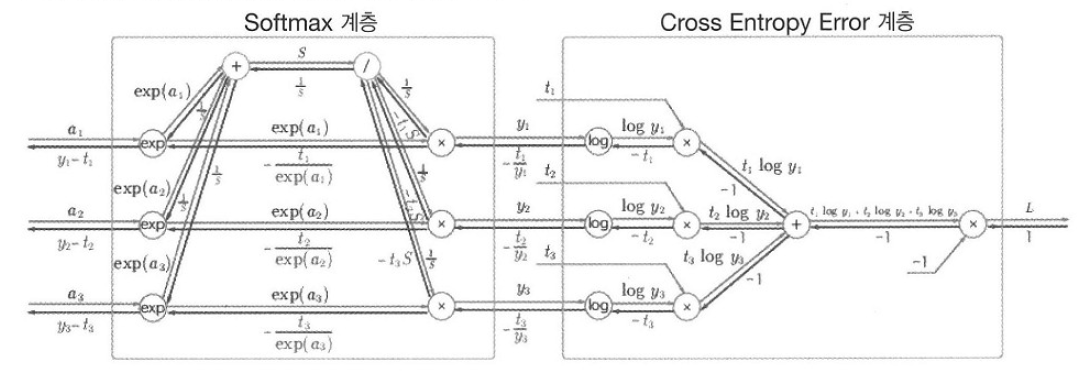
다소 복잡해보이지만 지금까지 본 연산들의 역전파와 다음 두 가지 사항을 보고 차근차근 역으로 올라가면 이해할 수 있습니다.
- Log함수의 역전파는 다음 층(역전파 순서)의 변수를 나눠주는 것이다.
- 순전파 때 한 노드에서 두 가지 갈래로 나뉘었다면, 역전파에서는 두 신호를 합쳐준 후 연쇄 법칙을 적용한다.
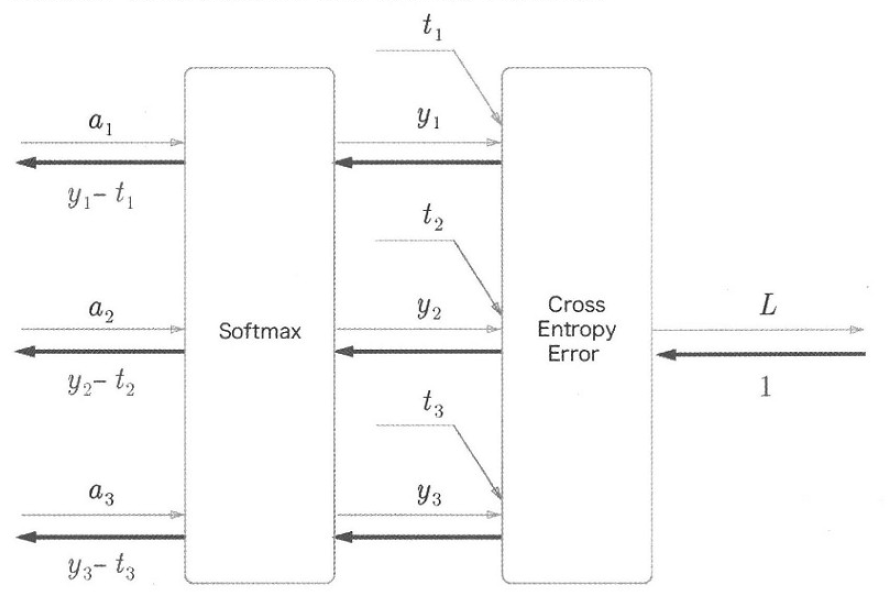
위 그림에서 "소프트맥스 함수 + 교차 엔트로피 오차"를 역전파하면 정답레이블과 신경망의 출력의 차이가 그대로 전해집니다. 이런 말끔함은 우연이 아니라 교차 엔트로피 오차가 그렇게 설게되었기 때문입니다. 또한 회귀의 출려긍에서 항등함수의 손실함수로 평균 제곱 오차를 이용하는 이유도 이와 같습니다.
오차역전파법의 완성
지금까지 살펴본 여러 역전파 계층들을 조합해서 전체 신경망의 오차역전파를 완성할 수 있습니다.
'AI_basic > Deeplearning' 카테고리의 다른 글
| [Deeplearning Part .6-1] CNN (1) | 2022.01.09 |
|---|---|
| [Deeplearning Part.5] 학습 관련 기술들 (0) | 2022.01.09 |
| [Deeplearning Part.3] 신경망 학습 (0) | 2022.01.06 |
| [Deeplearning Part.2] 신경망 (0) | 2022.01.05 |
| [Deeplearning Part.1]퍼셉트론과 단순 논리 회로 (0) | 2022.01.05 |



