보통 데이터셋은 여러 개의 설명변수를 가지고 있다. 데이터셋의 크기가 충분히 클 때 변수의 증가는 새로운 패턴을 발견하며 데이터셋을 더 정밀하게 설명할 수 있는 수단이 된다. 하지만 설명변수가 많아질 수록 좋은 것은 아니다. 오히려 알고리즘의 성능이 저하되는 현상이 생길 수 있다. 이러한 현상을 차원의 저주라고 한다.
차원의 저주
각 데이터(행)을 설명하는 변수가 늘어날 수록, 데이터 간의 거리가 멀어져 각 차원 별로 같은 영역의 자료를 갖고 있지만 전체 영역에서 설명할 수 있는 데이터의 비율은 즐어드는 'Sparsity'현상이 발생한다.
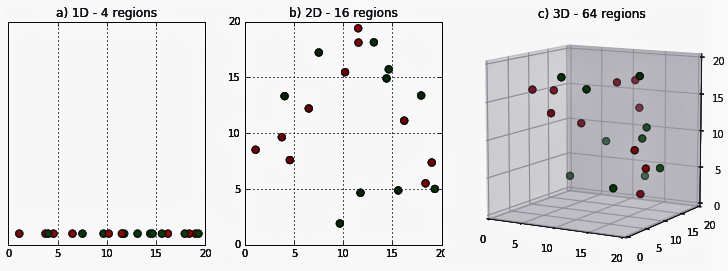
위 그림에서 오른쪽으로 갈 수록 차원이 하나씩 더 늘어난다. 각 차원축이 설명변수이므로, 차원이 늘어날 수록 데이터 간의 거리가 벌어지고 빈 공간이 증가한다.
이렇게 빈 공간이 증가할 수록, 각 차원의 일정 비율의 영역에서 설명할 수 있는 데이터는 줄어들게 되고, 이를 차원의 저주라고 한다.
1. 설명변수 선택
차원을 축소하는 가장 간단한 방법은 필요 없는 변수를 제거하는 것이다.
- 상관관계가 높은 변수
- 도메인 탐색 후 타겟을 설명하는데 상관 없을 것으로 판단되는 변수
성능 향상이 목표라면, 평가지표를 통해 설명변수를 선택하는데 다양한 실험을 거치는 것이 좋은 것 같다
2. 주성분 분석
주성분분석(PCA : Principle Component Analysis)은 차원축소에 가장 많이 사용되는 방법이다. 차원 추출은 기존의 설명변수들을 저차원(축소 시 설명변수 개수)의 초평면에 우영하는 것이다. 이 때 각 설명변수 간의 상관관계를 이용해 데이터를 축에 사영했을 때 분산이 가장 높은 축을 찾아 그 축을 새로운 주성분으로 결정하는 방법이다.

위 그림처럼 가장 큰 분산을 기반으로 첫 번째 축을 생성하고, 해당 벡터 축에 직각이 되는 벡터를 두 번째 축으로 선정한다. 같은 방법으로 그 다음 축도 정한다.
PCA 진행 시 각 설명변수의 스케일이 차이가 날 경우 주성분 선정에 영향을 주기 때문에 이상치 제거와 스케일링 이후에 PCA를 진행한다.
주성분 개수 정하기
- 설명력이 가장 큰 주성분부터 누적 분산 설명력이 0.8 넘어가게 되는 주성분까지 선정
- Scree Plot을 통해 기울기(분산의 변화 정도)가 급격히 감소하는 지점 직전까지의 주성분
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
iris_load = load_iris()
iris = pd.DataFrame(iris_load.data, columns = iris_load.feature_names)
iris['Class'] = load_iris().target
iris['Class'] = iris['Class'].map({0:'Setosa', 1:'Versicolour', 2:'Virginica'})
# 이상치 제거
def outliers_iqr(df, col, k):
q1, q3 = np.percentile(df[col], [25, 75])
iqr = q3 - q1
lower_whis = q1 - iqr*k
upper_whis = q3 + iqr*k
outliers = df[(df[col] > upper_whis) | (df[col] < lower_whis)]
return lower_whis, upper_whis, outliers[[col]]
for col in iris.columns:
if col == 'Class':
continue
lower_whis, upper_whis, outliers = outliers_iqr(iris, col, 1.5)
values = iris[col].values
values = np.clip(values, lower_whis, upper_whis)
iris[col] = values
# 데이터 분할
df = iris.drop(columns = 'Class')
target = iris['Class']
X_train, X_test, y_train, y_test = train_test_split(df, target, test_size = 0.2, random_state=42)
# 스케일링
SScaler = StandardScaler()
SScaler.fit(X_train)
X_train = SScaler.transform(X_train)
X_test = SScaler.transform(X_test)
# PCA
from sklearn.decomposition import PCA
pca = PCA(n_components = 4)
pca.fit(X_train)
print('분산 설명력 : ', pca.explained_variance_ratio_)
print('누적 분산 설명력 : ', [sum(pca.explained_variance_ratio_[:idx]) for idx in range(1, 5)])
plt.title('Scree Plot')
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explatined Variacne')
plt.plot(pca.explained_variance_ratio_, 'o-')
plt.show()
새로운 데이터프레임 생성
pca = PCA(n_components = 2)
pca_df = pd.DataFrame(data = pca.fit_transform(X_train), columns = ['Pc1', 'Pc2'])
pca_df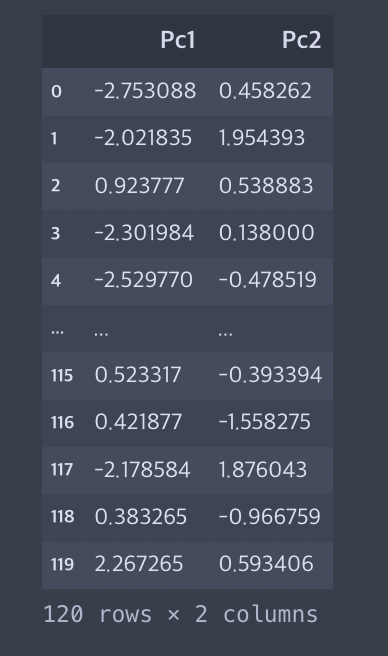
주성분 산포도 확인(target에 따라)
import seaborn as sns
plt.title('2 components PCA')
sns.scatterplot(x = 'Pc1', y = 'Pc2', hue = iris.Class, data = pca_df)
plt.show()
'ADP로ML정리' 카테고리의 다른 글
| 3. 머신러닝 평가지표 (0) | 2024.02.15 |
|---|---|
| 2-6. 데이터 전처리 - 데이터 불균형 문제 해결 (1) | 2024.02.15 |
| 2-4. 데이터 전처리 - 데이터 분할 및 스케일링 (1) | 2024.02.14 |
| 2-3. 데이터 전처리 - 범주형 변수 처리 (0) | 2024.02.14 |
| 2-2. 데이터 전처리 - 이상치 처리 (0) | 2024.02.14 |



