반응형
회귀분석
1. MAE(Mean Absolute Error)
- 실제값과 예측값의 차이의 절대값의 평균
- 에러의 크기가 그대로 반영됨
- 이상치에 영향을 받음

2. MSE(Mean Squared Error)
- 실제값과 예측값의 차이를 제곱한 평균
- 실제값과 예측값 차이의 면적 합을 의미
- 특이값이 존재하면 수치가 증가

3.RMSE(Root Mean Squared Error)
- 실제값과 예측값의 차이를 제곱해 평균한 것의 제곱근
- 에러에 제곱을 하면 에러가 클수록 그에 따른 가중치가 높이 반영
- 이때 손실이 기하급수적으로 증가하는 사오항에서 실제 오류평균보다 값이 더 커지지 않도록 상쇄하기 위해 사용

4. MSLE(Mean Squared Log Error)
- 실제값과 예측값의 차이를 제곱해 평균한 것에 로그 적용
- RMSE와 같이 손실이 기하급수적으로 증가하는 상황에서 실제 오류평균보다 값이 더 커지지 않도록 상쇄하기 위해 사용

5. MAPE(Mean Absolute Percentage Error)
- MAE를 퍼센트로 변환한 것
- 실제 정답보다 낮게 예측했는지 높게 예측했는지 파악하기 힘듦
- 실제 정답이 1보다 작을 경우 무한대의 값으로 수렴함

from sklearn.metrics import mean_absolute_error, mean_squared_error, mean_squared_log_error
import numpy as np
test = np.random.rand(100)
pred = np.random.rand(100)
mse = mean_squared_error(test, pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(test, pred)
msle = mean_squared_log_error(test, pred)
mape = np.mean(np.abs((test-pred)/test)) * 100
df = pd.DataFrame(index = ['mse', 'rmse', 'mae', 'msle', 'mape'])
df['metrics'] = [mse, rmse, mae, msle, mape]
df
분류분석
1. 정확도
- 실제 데이터에서 예측 데이터가 얼마나 같은지 판단하는 지표
- 데이터 구성에 따라 모델의 성능을 왜곡할 가능성이 있음(데이터 불균형 등)
2. Confusion Matrix
- 이진 분류에서 나올 수 있는지 4가지 경우에 대한 지표


- 여기서 Positive는 해당 task에서 분류해 내려는 레이블이다.
- 따라서 암 진단을 할 경우, 암이 양성이 경우를 분류해내려는 것이기 때문에 암이 양성이 경우를 Positive로 한다.
3. 정밀도 (Precision)
- Positive로 예측한 것 중 실제로도 Positive인 것들의 비율
- '정밀도'라는 단어의 뜻을 생각하면, 예측이 얼마나 정밀한가 -> 에측한 값 중 맞는 것이 얼마나 되는가?
- Negative를 Positive로 잘못 예측했을 때 부정적인 영향이 크게 발생할 때 주로 사용된다.
- ex) 일반 메일을 스팸 메일로 분류할 경우
4. 재현율(Recall)
- 실제 Positive인 것들 중 Positive로 예측한 것들의 비율
- '재현율'이라는 단어의 뜻을 생각하면, 실제를 얼마나 재현했는가 -> 실제값들 중 예측해낸 값이 얼마나 되는가?
- 민감도(Sensitivity) 또는 TPR(True Positive Rate)라고도 불림
- 실제 Positive인 경우를 Negative로 잘못 예측했을 때 부정적인 영향이 크게 발생할 때 주로 사용된다.
- ex) 암이 양성인 경우를 음성으로 진단했을 때
5. F1 score
- 정밀도와 재현율의 조화평균으로, 적절한 조화를 이룰 때 상대적으로 높은 수치를 나타냄

6. ROC curve & AUC score
- Roc curve는 FPR(False Positive Rate)이 변할 때 TPR(True Positive Rate)(Recall)이 변하는 것을 나타내는 곡선
- 여기서 FPR은 1-특이도(Specificity)인데, 특이도는 Negative 관점에서의 Recall. 즉 실제 Negative 중 예측값이 맞는 비율이다.
- 따라서 FPR은 실제 Negative 중 Positive로 예측한 비율이다.
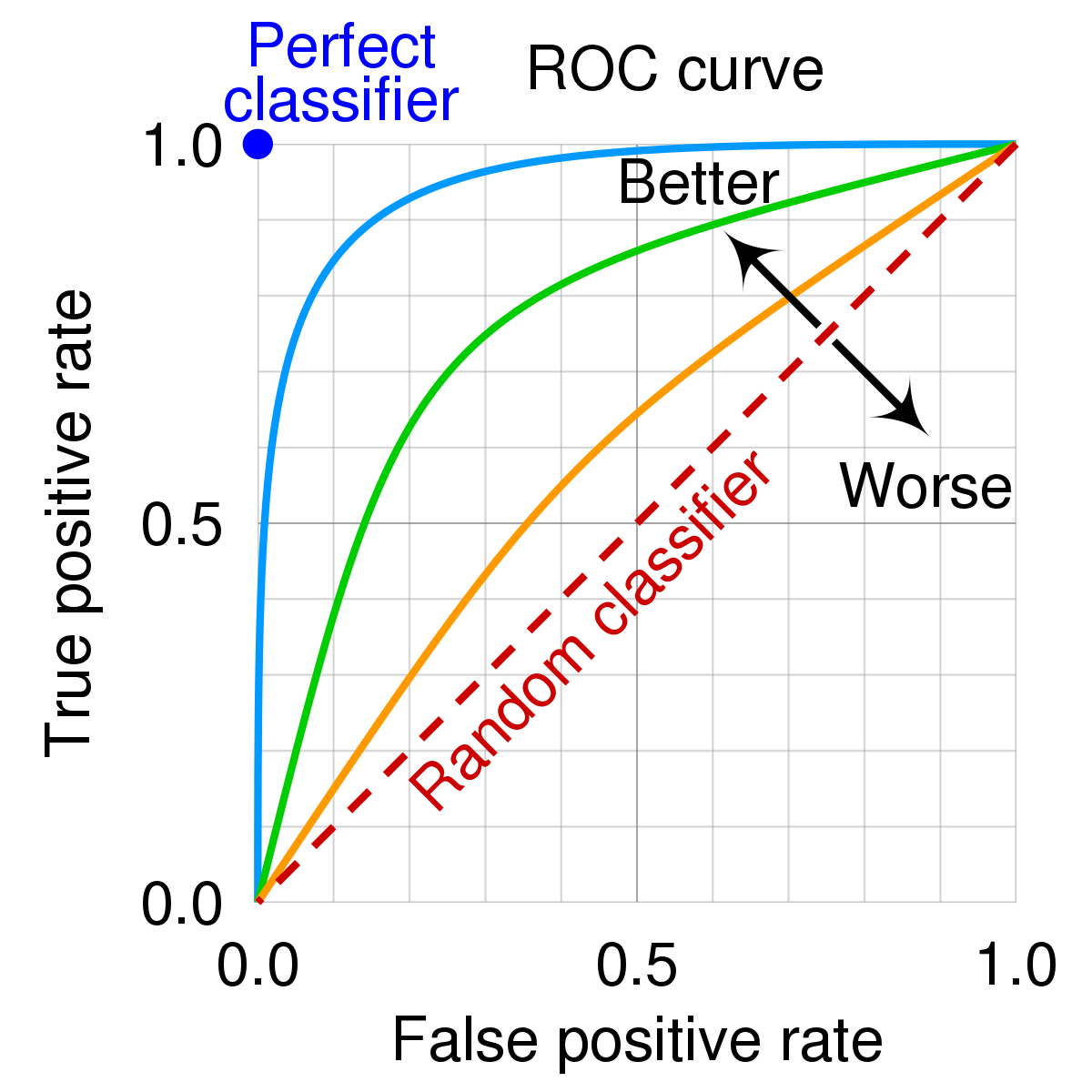
- AUC는 Area under Curve로, ROC curve 아래 영역의 면접이다.
- TPR은 클 수록 좋고, FPR은 작을 수록 좋다.
- TPR(Recall)이 크다 -> Positive로 예측한 값이 많다 -> 실제 Negative 중 Positive로 예측한 값이 많아졌을 수도?
- 실제 Negative 중 Positive로 예측한 값 -> FPR!
- 따라서 TPR이 크면서 FPR이 작으면 좋다!
- ROC curve 아래의 면적을 구하면, TPR이 커지면서 FPR이 작아지는 정도를 AUC로 측정할 수 있게 된다.
- AUC는 면적이기 때문에 0 ~ 1의 값을 갖고, 각 범위마다 보통 아래와 같은 평가르 한다.

from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.metrics import precision_score, recall_score, f1_score, roc_curve, auc
import matplotlib.pyplot as plt
test = np.round(np.random.rand(1000))
pred = np.round(np.random.rand(1000))
acc = accuracy_score(test, pred)
pre = precision_score(test, pred)
rec = recall_score(test, pred)
f1 = f1_score(test, pred)
fpr, tpr, thres = roc_curve(test, pred, pos_label=1)
auc = auc(fpr, tpr)
df = pd.DataFrame(index = ['Accuracy', 'Precision', 'Recall', 'F1', 'AUC'])
df['metrics'] = [acc, pre, rec, f1, auc]
print(df)
print('\n')
print(confusion_matrix(test, pred))
반응형
'ADP로ML정리' 카테고리의 다른 글
| 4-2. 회귀 모델 - 분류를 위한 회귀 모델 (1) | 2024.02.19 |
|---|---|
| 4-1. 회귀 모델 - 규제가 있는 선형 회귀 (1) | 2024.02.19 |
| 2-6. 데이터 전처리 - 데이터 불균형 문제 해결 (1) | 2024.02.15 |
| 2-5. 데이터 전처리 - 차원축소 (0) | 2024.02.14 |
| 2-4. 데이터 전처리 - 데이터 분할 및 스케일링 (1) | 2024.02.14 |



