반응형
F-분포
F-분포 카이제곱분포와 같이 분산을 이용하여 추정하고 검정하기 위해 고안된 확률분포이다. F분포는 2개 이상의 표본평균들이 동일한 모평균을 가진 집잔에서 추출되었는지 아니면 다른 모집단에서 추출된 것인지 판단하기 위하여 사용한다. 두 확률변수 V1, V2는 각각 자유도가 k1, k2이고 서로 독립인 카이제곱분포를 따를 때, 다음과 같이 정의되는 확률변수 F는 자유도가 (K1, k2)인 F-분포를 따른다고 한다.
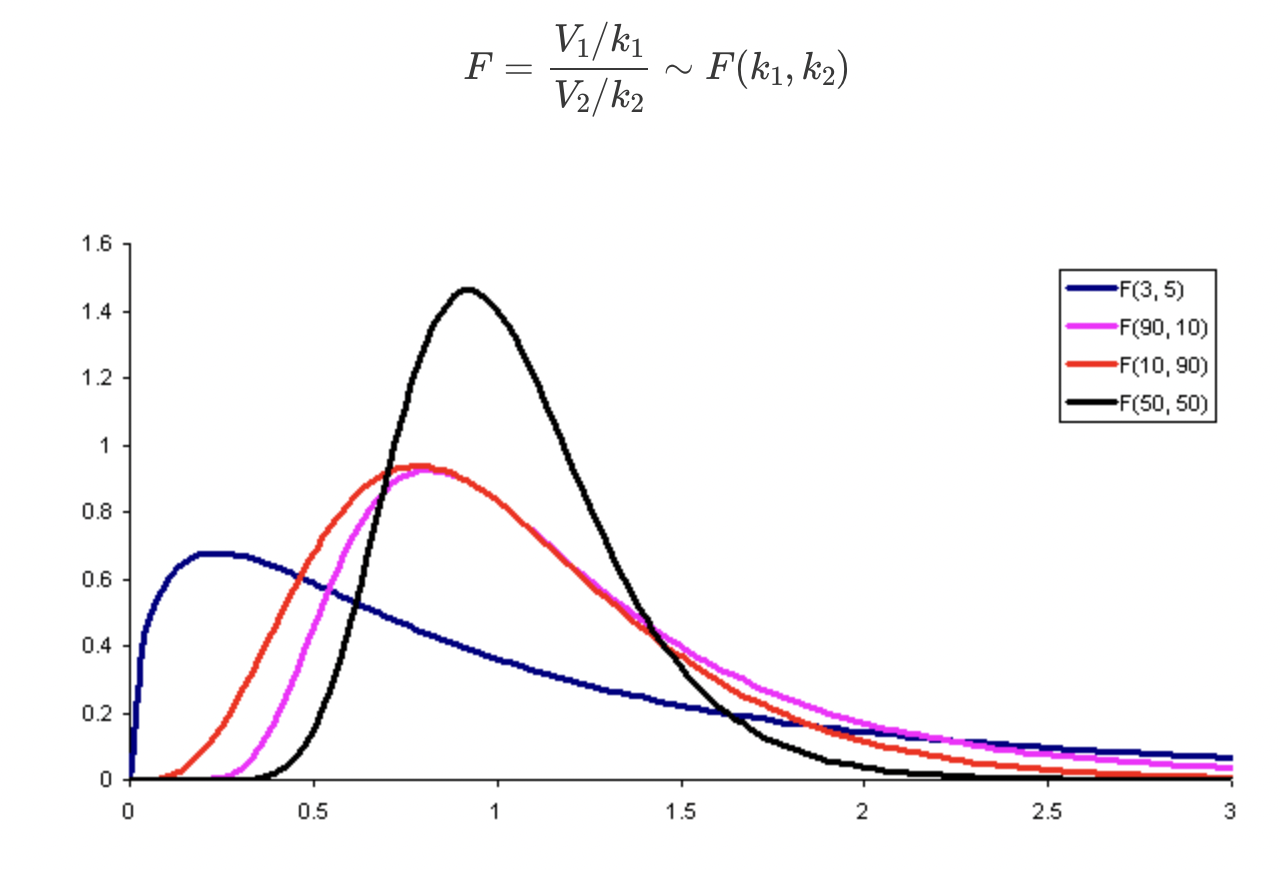
정리하면 F-분포는 2개의 카이제곱분포의 비율의 확률분포를 의미한다.
데이터들의 집합이 2개 이상일 때, 집합들의 평균의 분산을 얻을 수 있다. 이 때 F-값은 아래와 같다.

F-분포의 특성
- F분포는 카이제곱분포와 마찬가지로 좌우대칭이 아니다.
- 표준정규분포를 제곱하여 합한 카이제곱분포 2개를 서로 나눈 값이므로, 0보다 큰 영역에서만 그려진다.
- F(k1,k2)와 1 / F(k2,k1)는 동일한 분포를 가진다.
- 자유도가 n인 t분포를 제곱하면 F(1, n)인 F분포가 된다.
F-분포의 활용
- 일반적으로 두 분포의 분산을 비교하는데 활용된다.
- ANOVA에서 그룹 내 변동과 그룹 간 변동으로 여러 개의 평균값을 비교하는데 활용된다.
- 회귀분석에서 t분포는 개별 회귀계수의 유의성을 검정하는데 쓰이고, 회귀모형 자체의 유의성 검정으 위해서는 F분포가 쓰인다.
반응형
'Statistics' 카테고리의 다른 글
| 일표본(One-sample) 검정(feat.Python) (0) | 2024.01.16 |
|---|---|
| 추정과 가설 검정 간단 정리 (0) | 2024.01.15 |
| t-분포(t-distribution, Student's t-distribution) (1) | 2024.01.12 |
| 카이제곱분포(Chi-Square distribution) (0) | 2024.01.12 |
| 정규분포(Normal distribution) (0) | 2024.01.12 |



