모평균의 추정과 가설 검정 : Z분포, t분포
1. Z검정 - 표본의 크기가 30 이상이거나 모집단의 분산을 아는 경우
ex) 건전지의 평균 수명이 300일이라고 알려져있을 때, 일부에서 300일이 아니라는 의견이 나오고 있다. 해당 건전지 25개를 표본으로 뽑아 조사하였더니, 평균수명은 310일이 나왔고, 그 동안 수집한 자료를 분석한 결과 표준편차는 30일 이라고 한다. 이 때 어느 의견이 더 타당한지 유의수준 5%에서 검정하라.
원래 평균수명이 300일이라고 알려져있는데, 이것이 맞는지 검정하기 위한 것이므로 평균수명=300일 을 귀무가설로 설정하고, 평균수명은 300일이 아니다를 대립가설로 설정한다.

알려져 있는 표본개수, 모평균과 표본평균을 대입해 검정통계량을 계산하면 1.67이 나온다. 이 때 대립가설이 "이상, 이하"를 가정한 것이 아닌 "아니다"라는 가정으로 양측 검정을 실시하게 되는데, Z분포표를 통해 양측에서 0.05를 차지(한 쪽에서 0.025)하는 기각역을 찾는다. 이 때 Z분포표에서 찾아내는 값(1.96)이 오른쪽 측면의 임계값이 된다.

위 Z분포표 내의 값들은 Z분포의 왼쪽 끝에서부터 차지 하는 면적이다. 따라서 오른쪽 0.025를 차지하는 임계값을 구하기 위해서는 왼쪽부터 0.975를 차지하는 면적의 임계값을 찾는다. 이 때 양측의 임계값은 ±1.96이 된다. 해당 임계값을 통해 계산한 기각역과 채택역을 보면, 검정통계량(1.67)이 채택역에 위치하므로 귀무가설을 기각할 수 없다. 따라서 건전지의 평균수명은 300일이 아니라고 할 수 없다.
### 모분산을 아는 경우의 모평균의 추정
import numpy as np
from scipy.stats import norm
x_hat = 310 #표본평균
mu0 = 300 # 귀무가설의 모평균
n = 25 # 표본개수
sigma = 30 #모표준푠차
conf_a = 0.05 # 유의수준 (신뢰수준 95% 기준)
SE = sigma/np.sqrt(n) # standard error
zstat = (x_hat - mu0) / SE # Z검정통계량
# 양측 검정에 따른 유의확률과 임계값
ways = 'two' # "two", 'one-right', 'one-left'
sp = (1 - norm.cdf(np.abs(zstat)))*2 # 유의확률
cv = norm.ppf(1-conf_a/2) # 임계값
print("[검정]")
print(f"임계값 : +/-{cv:.3f}, 검정통계량 : {zstat:.2f}")
if zstat<cv and zstat>-cv:
print('귀무가설을 기각할 수 없음 = 평균이 300이 아니라고 할 수 없음')
else:
print('귀무가설을 기각하고, 대립가설을 채택함 = 평균이 300이 아니라고 할 수 있음')
2. t검정(일표본 t검정) - 표본의 크기가 30 미만이고 모집단의 분산을 모르는 경우
ex) 어느 과자 회사의 과자는 40g인데, 소비자들로부터 40g 보다 적다는 불평이 쏟아졌다. 그래서 어느 주장이 더 타당한지 파악하기 위해 과자 8봉지를 표본으로 뽑았더니, 평균 무게는 39g이 나왔고 표준편차는 5g이 나왔다. 이 때 어느 주장이 더 타당한지 유의수준 5%에서 검정하시오.
대립가설로 시멘트의 평균무게가 40g보다 적을 것이라는 주장이 나왔으므로, 대립가설은 "과자 무게는 40g 보다 작다"로 설정한다. 자동으로 귀무가설은 과자 무게가 40g보다 클 것이다로 정해진다.

t 통계량 공식을 사용해 t검정통계량이 -0.57로 구해졌다.

"작다"라는 단측 검정을 실시해야하므로 t분포에서 자유도 7(8-1), 유의수준 0.05의 임계값을 구하면 1.895가 나온다. "작다"라는 단측 검정을 위해 왼쪽 측면 임계값 -1.895를 대입해 기각역을 구하면, 검정통계량 -0.57은 채택역 안에 위치하므로 귀무가설을 기각할 수 없다. 따라서 과자의 무게는 40g보다 적다고 할 수 없다.
### 모분산을 모르고 표본의 크기가 30 미만일 경우의 모평균의 추정
import numpy as np
from scipy.stats import t
x_hat = 39 #표본평균
mu0 = 40 # 귀무가설의 모평균
n = 8 # 표본개수
df = n-1 # 자유도
s = 5 # 표본표준푠차
conf_a = 0.05 # 유의수준 (신뢰수준 95% 기준)
SE = s/np.sqrt(n) # standard error
tstat = (x_hat - mu0) / SE # t검정통계량
# 단측 검정에 따른 유의확률과 임계값
ways = 'one-left' # "two", 'one-right', 'one-left'
sp = t.cdf(tstat, df) #유의확률
cv = t.ppf(conf_a, df) #임계값
print("[검정]")
print(f"임계값 : {cv:.3f}, 검정통계량 : {tstat:.2f}")
if zstat>cv:
print('귀무가설을 기각할 수 없음 = 평균이 40g 보다 적다고 할 수 없음')
else:
print('귀무가설을 기각하고, 대립가설을 채택함 = 평균이 40g 보다 적다고 할 수 있음')
3. 일표본 검정의 정규성 검정
대부분의 모수 검정법은 기본 가정사항을 만족해야하는데, 기본 가정을 만족하지 못하면 비모수 검정으로 분석하여야 한다. 통계를 모르는 많은 연구자들은 t검정을 사용하였다고 기본 가정사항을 확인하지 않고 무조건 따라 하는 경향이 있는데, 이는 잘못된 분석이다.
일표본 t검정의 기본 가정사항은 "정규성" 하나만 존재한다. 보통 표본 수가 30개 이상이면 중심극한정리에 의해 정규성을 만족하는 것으로 보고 있다.
정규성 검정을 하는 이유는?
- 단순히 정규 모집단이 맞는지 확인하기 위해서
- 정규 모집단이라는 것이 확인되면 모수 검정을 하고, 아니면 비모수 검정을 하기 위해서
1은 통계학을 전공하는 사람들에게나 관심이 있는 것이고, 대부분의 연구자들은 2에 그 목적이 있다.
2의 목적을 위해 연구자들은 흔히 Shapiro-Wilk 등의 정규성 검정을 한 후, p-value가 0.05보다 작게 나타나면 정규 모집단이 아니라는 결론을 내리고 비모수 검정을 선택하고, 더 크게 나타나면 모수 검정을 진행한다.
여기서 중심극한 정리를 살펴 보면, "모집단이 정규분포가 아닌 경우에도 표본의 수가 충분히 크면 표본 평균의 분포는 근사적으로 정규분포에 따른다"라는 이론이다. 이에 따라 만약 표본 수가 충분히 크다면 정규 모집단이라는 가정도 필요 없이 Z검정으로 평균을 비교해도 된다.
따라서 겅규성 검정의 목적이 2라면, 표본 수가 충분히 큰 경우에는 정규성 검정을 할 필요 없이 바로 모수 검정을 선택하면 된다. 하지만 표본의 크기가 30미만일 경우, 정규성 검정을 필요로한다. 정규성 검정은 Holmogorov-Smirnove 검정과 Shapiro-Wilk 검정을 통해 쉽게 확인할 수 있다.
모비율의 추정과 가설 검정: Z분포
모비율의 가설검정은 "모비율인 p가 이럴 것이다"라고 설정된 귀무가설과 대립가설 중에서, 하나의 가설을 선택하는 것이다. 모비율의 가설검정은 기본적으로 표준정규분포를 사용한다.
ex) 우리나라 성인 남자의 43%는 안경을 끼는 것으로 알려져 있는데, 최근 라식/라섹 기술 발전으로 안경을 쓰는 비율이 43%보다 낮아졌을 것이라는 의견이 나왔다. 이에 실제로 어떠한지를 알아보기 위해서 성인 남자 1000명을 뽑아 조사했더니 안경을 낀 사람은 420명이었다. 이 때 안경을 낀 비율이 43%보다 낮아졌다고 할 수 있는지 유의수준 10%에서 검정하시오.
안경을 낀 비율이 43%보다 낮아졌을 것이라는 의견을 확인하고 싶으므로 "안경을 낀 비율은 43%보다 낮다"를 대립가설로 설정하고, "43%보다 낮아지지 않았다"를 귀무가설로 설정한다.
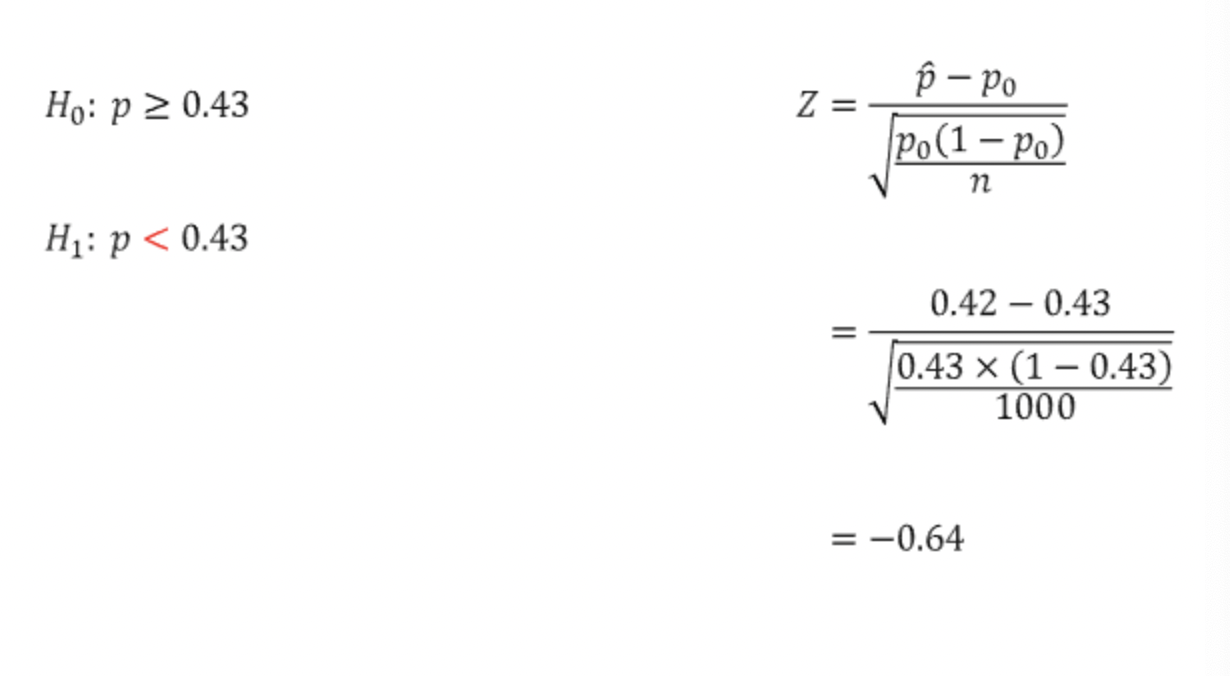
모비율의 추정을 위한 Z검정식을 통해 검정통계량을 구하면 -0.64가 나온다. 유의수준 0.1의 Z값(임계값)은 1.28이고, "낮다"라는 대립가설을 주장하기 위해 왼쪽 측면 단측 검정을 실시하기 위한 임계값은 -1.28이다.
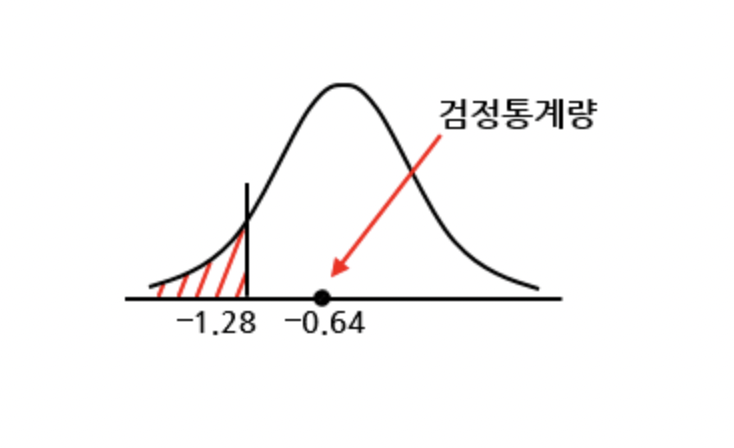
이 때 검정통계량은 채택역에 위치하므로 귀무가설을 기각할 수 없다. 따라서 성인 남자의 안경을 낀 비율이 43%보다 낮아졌다고 할 수 없다.
### 모비율의 가설검정
import numpy as np
from scipy.stats import norm
n = 1000 # 표본 개수
p = 420/n #표본 비율
P0 = 0.43 #귀무가설의 모비율
test_a = 0.1
SE = np.sqrt(P0*(1-P0)/n) #귀무가설의 모비율로 SE 계산
zstat = (p-P0)/SE
# 단측 검정에 따른 유의확률과 임계값
ways = 'one-left' # "two", 'one-right', 'one-left'
sp = norm.cdf(zstat) #유의확률
cv = norm.ppf(test_a) #임계값
print("[검정]")
print(f"임계값 : {cv:.3f}, 검정통계량 : {tstat:.2f}")
if zstat>cv:
print('귀무가설을 기각할 수 없음 = 모비율이 43% 보다 낮아졌다고 할 수 없음')
else:
print('귀무가설을 기각하고, 대립가설을 채택함 = 모비율이 43% 보다 낮아졌다고 할 수 있음')
모분산의 추정과 가설 검정: 카이제곱분포
모분산의 가설검정은 '모분산이 이럴 것이다'라고 가정한 귀무가설과 대립가설 중에서 하나의 가설을 채택하는 것인데, 위에서 다룬 모평균과 모비율에 대한 가설검정과 흐름은 비슷하다.
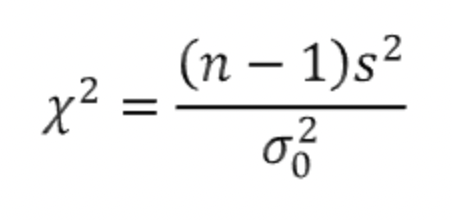
ex) 전국 고등학생들의 성적의 분산은 25라고 알려져 있는데, 최근에 학업 외 진로를 찾은 학생들이 많이 성적이 낮아져 분산이 25보다 클 수도 있다는 의견이 나왔다. 실제로 분산이 어떠한지 알아보기 위해 학생들 표본 10명을 뽑았더니 표본분산은 29가 나왔다. 그럼 전국 학생들의 성적의 분산이 25보다 크다고 할 수 있는지 유의수준 5%에서 검정하시오.
대립가설로 분산이 25보다 클 수도 있다는 의견이 나왔으므로 대립가설은 "분산이 25보다 크다"로 설정하고, 귀무가설은 그 반대이다.
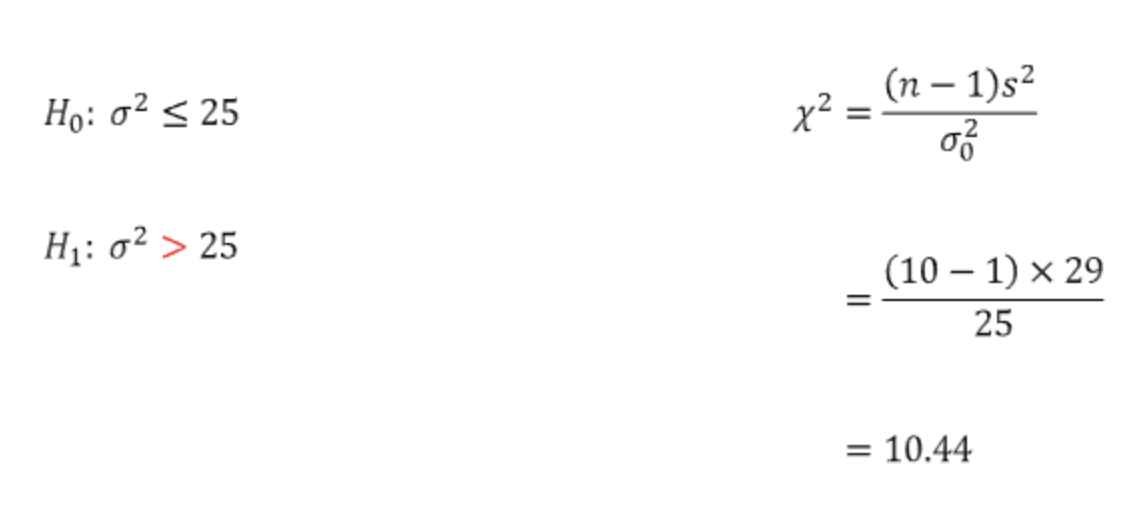
검정통계량을 구하면 10.44가 나오고, 유의수준 5%에 자유도9에 해당하는 값을 카이제곱분포표에서 찾으면 아래와 같이 16.92가 나온다.
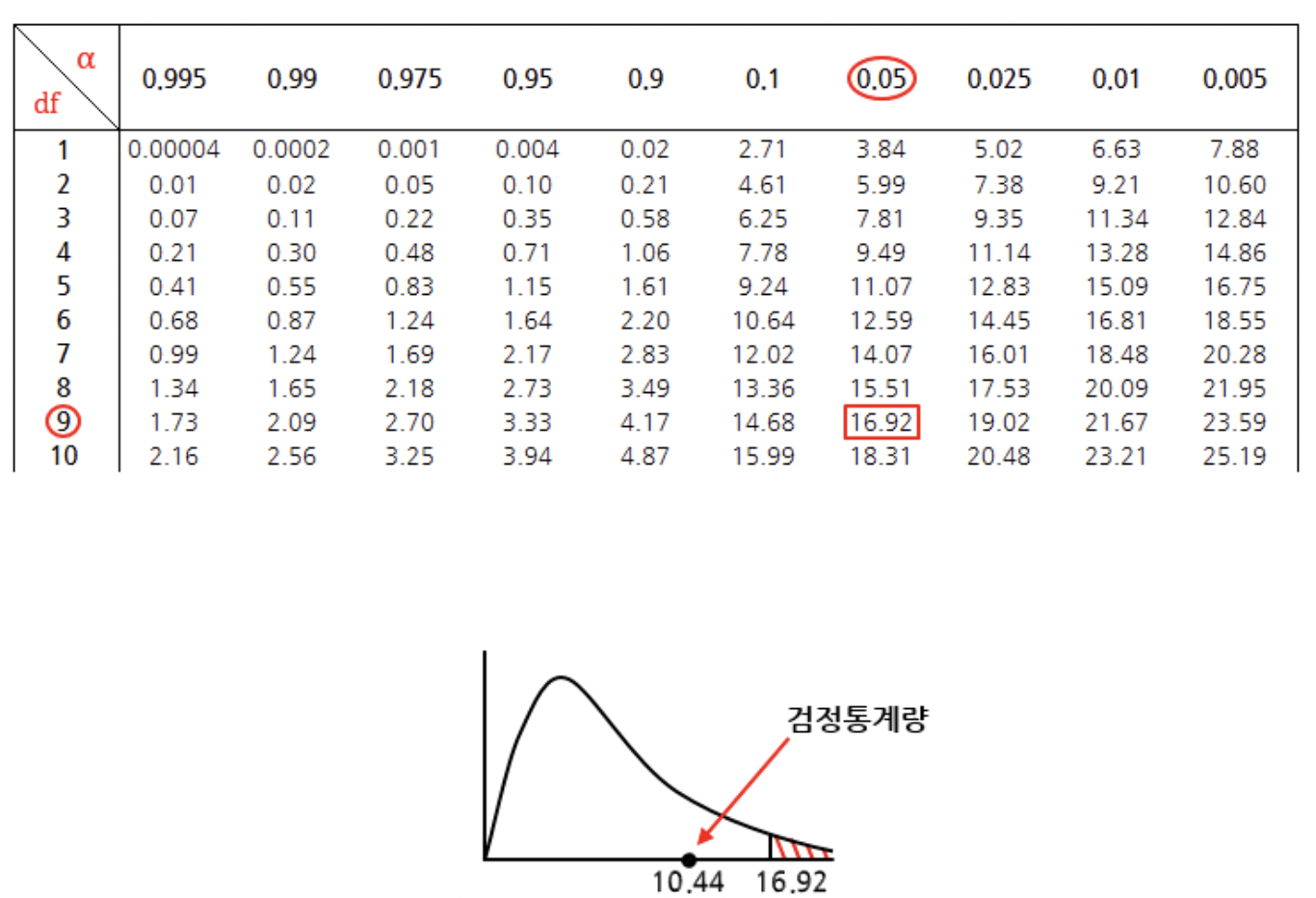
이 때 검정통계량이 채택역에 위치하므로 귀무가설을 기각할 수 없다. 따라서, "전국 학생들의 성적의 분산이 25보다 크다고 할 수 없다"
### 모분산의 가설검정
from scipy.stats import chi2
n = 10 #표본
v = 29 #표본분산
df = n-1 #자유도
v0 = 25 #귀무가설의 모분산
test_a = 0.05
cstat = df * v / v0 # 카이제곱통계량
# 단측 검정에 따른 유의확률과 임계값
sp = 1-chi2.cdf(cstat, df)
cv = chi2.ppf(1-test_a, df)
print("[검정]")
print(f"임계값 : {cv:.3f}, 검정통계량 : {cstat:.2f}")
if cstat<cv:
print('귀무가설을 기각할 수 없음 = 모분산이 25보다 높아졌다고 할 수 없음')
else:
print('귀무가설을 기각하고, 대립가설을 채택함 = 모분산이 25보다 낮아졌다고 할 수 있음')

'Statistics' 카테고리의 다른 글
| 분산분석(ANOVA)의 가정(feat.Python) (1) | 2024.01.18 |
|---|---|
| 이표본 검정(Two-sample)(feat.Python) (1) | 2024.01.17 |
| 추정과 가설 검정 간단 정리 (0) | 2024.01.15 |
| F-분포(F-distribution) (0) | 2024.01.12 |
| t-분포(t-distribution, Student's t-distribution) (1) | 2024.01.12 |



