두 모집단의 가설검정
일표본 검정과 달리, 두 모집단의 가설검정은 집단 각각의 모수가 어떠한 관계에 있는지를 검정한다. 이 때 두 모수의 관계는 보통 =, <, > 이렇게 3가지가 있는데, 서로의 관계를 파악할 때는 주로 뺄셈과 나눗셈을 사용한다.
- 모평균, 모비율의 비교 - 뺄셈을 사용해, [모수 - 모수]가 0, 음수, 양수 중 어떠한 값을 갖는지 가설로 설정한다.
- 모분산의 비교 - 나눗셈을 사용해 1, 1보다 큰 수, 1보다 작은 수 중 어떠한 값을 갖는지 가설로 설정한다.

이 때 모분산이 나눗셈을 사용하는 이유는 확률분포 때문인데, 모평균과 모비율은 뺄셈을 해도 정규분포나 t분포를 사용할 수 있지만, 모분산은 뺄셈을 하면 사용할 확률분포가 없기 때문이다.
또한 두 모집단의 두 모수의 크기가 서로 완벽하게 같을 확률은 거의 없다. 따라서 모수가 다르더라도 크게 차이가 나지 않으면 통계학에서는 서로 같다고 취급할 수 있다. 하지만 이 과정에서 정량적인 방법을 통해 검정통계량과 기각역을 구해서 서로 비교하는 번거로운 과정을 거친다.
독립표본 모평균 차이의 추정과 가설 검정: Z분포, t분포
1. Z검정 - 표본의 크기가 30 이상이고 모집단의 분산을 아는 경우

위 식에 따라 검정통계량을 계산하고 검정을 진행하면 되는데, 실제로 두 모집단의 분산이 알려져 있는 경우는 잘 없다고 한다. 또한 표본의 크기가 30이상이고 모집단의 분산을 모르는 경우는, 아는 경우와 같은 식에 모분산 대신 표본분산을 사용하면 된다.
여기에 대한 생각
- 두 모집단의 분산을 안다면? -> 전체 데이터와 모평균을 안다는 것인데 이러면 두 모평균 차이에 대한 가설 검정을 하는 것이 의미가 있나 싶다.
- 두 모집단의 분산을 아는데 분산을 계산하기 위한 전체 데이터와 모평균이 과거에 수집된 데이터이고, 대립가설로서 현재는 모평균이 다를 것이다는 주장아리면? -> 현재의 모분산을 모르기 때문에 모분산을 모른다는 가정으로 가설 검정 진행해야됌
2. 표본의 크기가 30 미만이고 모집단의 분산을 모르지만 두 모분산이 동일하다는 것을 알 때

두 모분산이 동일하다고 할 때 다음과 같이 통합분산추정량을 계산하여 사용한다. 통합분산추정량은 각 표본의 자유도를 가중치로 사용해서 구한 두 표본분산의 가중평균이다. 이것을 사용하는 이유는 데이터의 신뢰도를 올리기 위해서라고 한다.
또한 기각역을 구할 때 두 집단의 자유도를 더해 줘야 하는데(통합분산추정량의 분모), 이는 기각역을 1개만 만들기 위해서다. 자유도를 따로따로 계산하면 기각역이 2개가 생기기 때문이다.

이 때 t 검정통계량을 계산하는 방식은 Z 검정과 유사한데, 단지 두 집단의 모분산 대신 통합분산추정량을 사용하면 된다.
ex) 공대생과 인문대생의 월평균 독서량이 차이가 나는지 알아보려 공대생 10명과 인문대생 11명을 뽑아 월평균독서량을 조사하였더니 평균은 각각 5권과 7권, 표본분산은 각각 0.5권과 2권이 나왔다. 월평균독서량이 차이가 나는지를 유의수준 5% 에서 검정하시오.
차이가 나는지를 밝히고 싶기 때문에 대립가설은 "공대생과 인문대생의 월평균독서량은 같지 않다"로 설정한다.
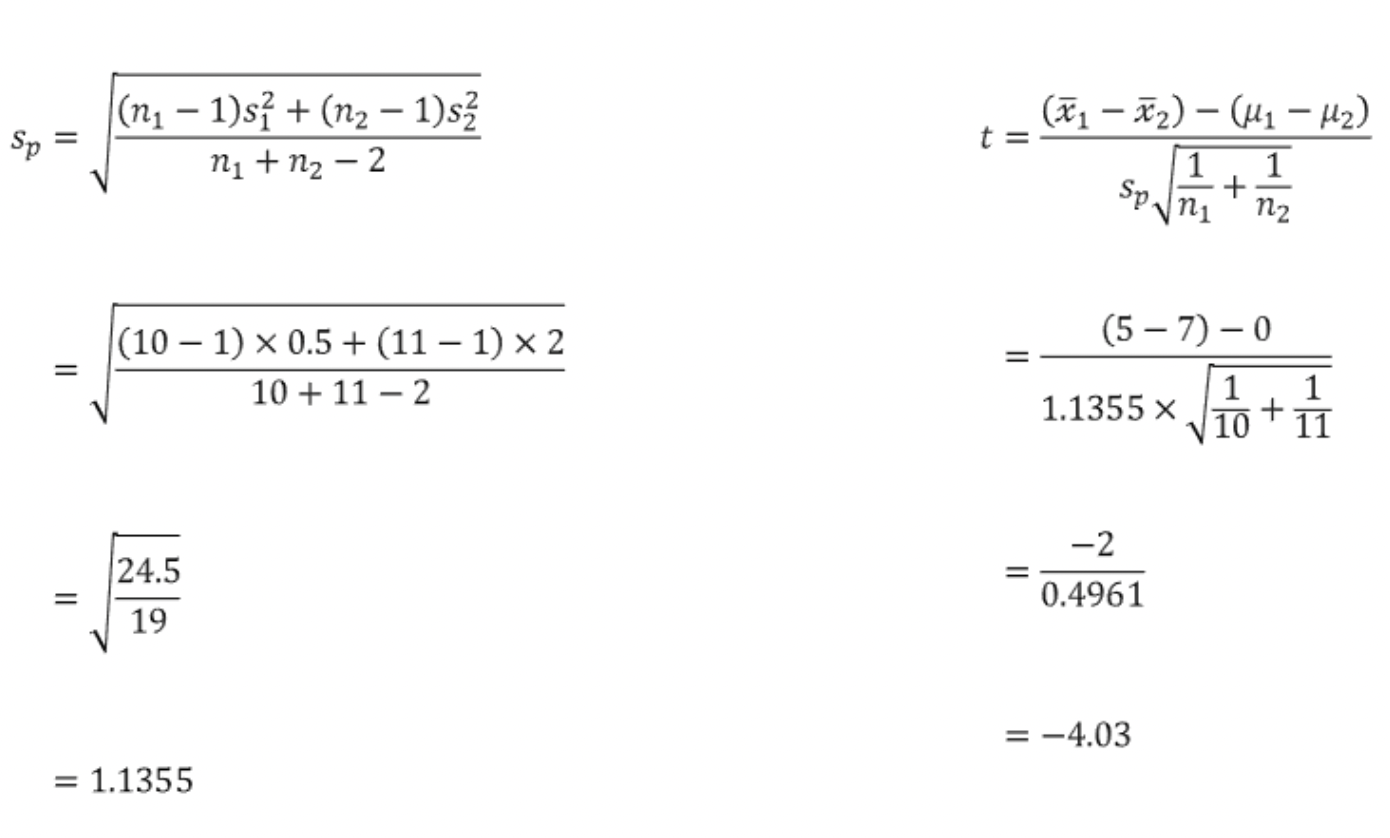
합동표준편차는 1.1355가 나오고 이를 통해 검정통계량을 계산하면 -4.03이 나온다. 유의수준 0.05에서 양측검정을 실시하면 다음과 같다.

자유도는 10+11-2=19이고 양측검정에 따라 0.025인 경우를 분포에서 찾으면 2.093이 나온다. 이 때 검정통게량이 기각역 안에 위치하므로 귀무가설을 기각한다. 따라서, "공대생과 인문대생의 월평균독서량은 차이가 난다고 할 수 있다."
### 표본의 크기가 30미만이고 모집단의 분산을 모르지만 같다는 것을 알고 있을 경우
# 독립표본 모평균 차이의 추정
from scipy.stats import t
import numpy as np
x1 = 5 #표본평균1
x2 = 7 #표본평균2
s1 = np.sqrt(0.5) #표본분산1
s2 = np.sqrt(2) #표본분산2
n1 = 10 #표본개수1
n2 = 11 #표본개수2
test_a = 0.05 #유의수준
d = x1 - x2 #두 표본평균의 차이
df = n1+n2-2 #자유도
pv = (s1**2*(n1-1) + s2**2*(n2-1))/df #통합분산추정량 pooled varance
SE = np.sqrt(pv) * np.sqrt(1/n1 + 1/n2)
tstat = (x1-x2-0)/SE
# 양측 검정에 따른 유의확률과 임계값
sp = (1-t.cdf(np.abs(tstat), df)) #유의확률
cv = t.ppf(1-test_a/2, df) #유의수준
print("[검정]")
print(f"임계값 : +-{cv:.3f}, 검정통계량 : {tstat:.2f}")
if tstat<cv and tstat>-cv:
print('귀무가설을 기각할 수 없음 = 모평균의 차이가 있다고 할 수 없음')
else:
print('귀무가설을 기각하고, 대립가설을 채택함 = 모평균이 차이가 난다고 할 수 있음')
3. 표본의 크기가 30 미만이고 모집단의 분산을 모르지만 두 모집단의 분산이 다르다는 것을 알고 있을 경우

이 경우 위와 같은 식을 통해 검정통계량을 계산하는데, 정규분포와 t분포를 따르지 않고 특정한 자유도를 지닌 t분포를 근사적으로 따른다고 한다. 해당 자유도는 다음과 같은 식으로 구한다.

대응표본의 가설검정
대응표본의 가설검정은 두 모평균의 가설검정과 비슷한데, 두 모평균의 가설검정은 2개의 집단에 대한 검정이었다면 대응표본의 가설검정은 1개의 집단을 대상으로 한다. 1개의 집단이기는 하지만, 실험 전 후에 따라 평균이 달라지므로 두 모평균의 가설검정과 비슷하다.(대응표본을 쌍체비교 혹은 짝표본이라고도 한다.)

대응표본 모평균 차이의 추정과 가설 검정
대응표본이 두 모평균의 가설검정과의 차이점은 검정통계량이다. 두 모평균은 두 집단을 다루지만 대응표본은 실험 전 후의 평균이 어떻게 달라지는지를 파악하기 때문에, 실험 전 후 차이의 평균과 표준편차를 알아야 검정통계량을 구할 수 있다. 또한 실험 전 후에 따른 차이만 있기 때문에 기본적으로 한 집단을 다루어 n만 사용한다.(표본의 개수 1개)

여기서 두 평균의 차(u1-u2)는 실험 전 후 차이가 나는지에 대한 가설에 따라 들어가는 값이고, 나머지 통계량(표본으로 부터 추출)은 실험 전 후의 "차이" 또한 "변화량"이므로 하나의 값들만이 들어간다.
ex) 어느 과외 선생이 학생들을 가르쳤을 때, 수업 전 후에 성적의 차이가 생기는지를 알아보려한다. 이에 학생 5명을 뽑아 수업 전 후 성적을 조사했더니 아래와 같이 나왔다. 수업 전 후에 성적의 차이가 생기는지 유의수준 10%에서 검정하시오.
수업 전 후 성적의 차이가 생기는지 밝히고 싶기 때문에 대립가설을 "수업 전 후 성적이 같지 않다"로 설정한다.

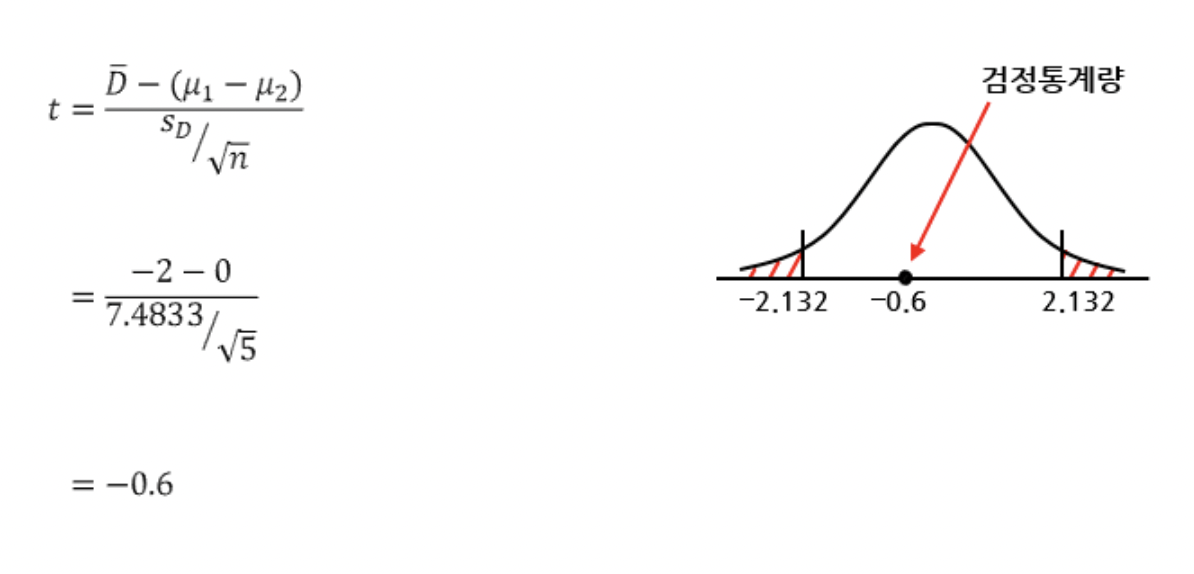
교육 전 후 차이의 평균은 -2, 차이의 표준편차는 7.4833으로 나왔다. 해당 값들을 통해 검정통계량을 계산하면 -0.6이 나온다. 유의수준 0.1과 자유도 5-1=4에서 임계값은 +-2.132이다. 검정통계량이 채택역 안에 위치하므로 귀무가설을 기각할 수 없다. 따라서 "수업을 한 전 후 성적의 차이가 있다고 할 수 없다."
### 표본의 크기가 30 미만인 경우 대응표본 모평균 차이의 추정
from scipy.stats import t
import numpy as np
a = np.array([60, 72, 45, 55, 70])
b = np.array([69, 65, 50, 63, 65])
test_a = 0.1 #유의수준
d0 = 0 #귀무가설의 평균 차이
d = a-b
n = 5 #표본개수
df = n-1 # 자유도
d_mean = np.mean(d) # 두 집단 차이의 평균
d_std = np.sqrt(1/df * sum((d-d_mean)**2)) # 두 집단 차이의 표준편차
SE = d_std / np.sqrt(n)
tstat = (d_mean-d0) / SE
# 양측 검정에 따른 유의확률과 임계값
sp = (1-t.cdf(np.abs(tstat), df))*2 #유의확률
cv = t.ppf(1-test_a/2, df) #유의수준
print("[검정]")
print(f"임계값 : +-{cv:.3f}, 검정통계량 : {tstat:.2f}")
if tstat<cv and tstat>-cv:
print('귀무가설을 기각할 수 없음 = 모평균의 차이가 있다고 할 수 없음')
else:
print('귀무가설을 기각하고, 대립가설을 채택함 = 모평균이 차이가 난다고 할 수 있음')
표본의 크기가 충분히 크고 실험 전 후의 모집단이 정규분포를 따른다면, 위의 검정통계량 계산식과 같은 식으로 Z검정을 진행하면 된다. 또한, python을 통해 가설 검정을 진행할 때 차이의 표준편차 계산 시 자유도가 n-1이므로 단순히 numpy의 표준편차 메소드를 사용하면 결과값이 달라질 수 있다.
두 모비율 차이의 추정과 가설검정
두 모비율의 가설검정은 "두 모비율의 관계가 이럴 것이다"라는 가설을 검정하게 되는데, 이 때 실제 모비율을 모르는 채로 두 모비율의 관계를 추정하는 것이기 때문에 검정통계량 계산에서 쓰이는 두 모비율은 가설 속의 모비율이다. 이 때 관계를 위해 뺄셈을 통해 같다라는 가정에 0이 대입할 수 있고, x 이상/이하 차이가 난다 등으로 응용할 수 있다.

또한 두 모비율이 같은지 다른지 아직 모르는 상황이지만 일반적으로 귀무가설을 p1=p2로 설정할 떄, 두 집단의 모비율이 같다는 가정임으로 검정통계량 계산 시 합동표본비율을 사용한다. 합동표본비율은 단순히 두 집단의 표본을 합쳐 비율을 구하면 된다.
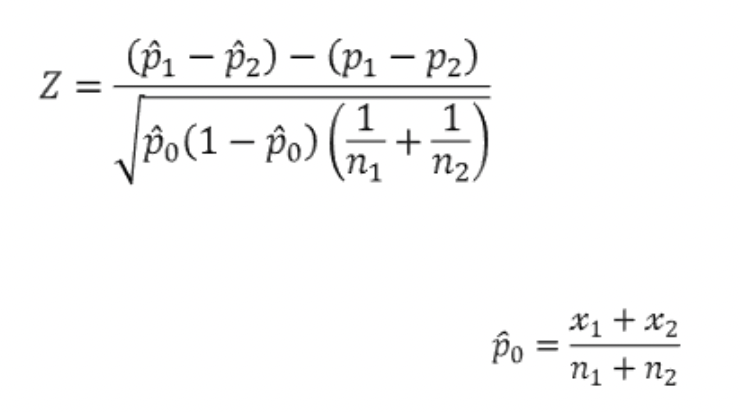
ex) 동일한 회사의 2개 공장에서 생산하는 제품의 불량률은 같은 것으로 알려져 있는데, 사실 불량률이 다를 수도 있다는 의견이 나오고 있어 실제로 어떠한지를 알아보기 위해 각각 표본 120개와 130개를 뽑은 결과 불량품은 각각 6개의 4개가 나왔다. 두 공장에서 생산하는 제품의 불량률이 서로 다르다고 할 수 있는지 유의수준 5%에서 검정하시오.
불량률이 다르다는 것을 밝히고 싶기 때문에 "두 공장의 불량률은 다르다"를 대립가설로 설정한다.
### 모비율의 차이의 추정과 가설 검정
from scipy.stats import norm
import numpy as np
test_a = 0.05 #유의수준
p = 0 # 귀무가설의 모비율 차이
n1 = 120 #표본개수1
n2 = 130 #표본개수2
p1 = np.round(6/n1, 2) #표본비율1
p2 = np.round(4/n2, 2) #표본비율2
p0 = (p1*n1 + p2*n2) / (n1 + n2) # 합동표본비율
zstat = (p1-p2-p)/np.sqrt(p0*(1-p0)*(1/n1 + 1/n2))
# 양측 검정에 따른 유의확률과 임계값
sp = (1-norm.cdf(np.abs(zstat)))*2 #유의확률
cv = norm.ppf(1-test_a/2) #유의수준
print("[검정]")
print(f"임계값 : +-{cv:.3f}, 검정통계량 : {zstat:.2f}")
if zstat<cv and zstat>-cv:
print('귀무가설을 기각할 수 없음 = 모비율의 차이가 있다고 할 수 없음')
else:
print('귀무가설을 기각하고, 대립가설을 채택함 = 모비율이 차이가 난다고 할 수 있음')
모분산 비의 추정과 가설 검정: F분포
2개의 모분산이 서로 어떠한 관계에 있는지를 비교하기 위해 나눗셈을 사용해 다음과 같이 가설을 설정할 수 있다.

또한 모비율 차이의 검정과 마찬가지로 귀무가설의 설정에 따라 검정통계량 식에 쓰이는 두 모분산의 비는 1로 설정해 생략하면 된다(두 모분산이 x배 차이가 난다, 등 응용을 통해 다양한 가정을 할 수 있지만 일반적으로 잘 하지 않는다). 따라서 검정통계량인 F의 결과는 두 표본표분산의 비이다.

또한 F분포표를 통해 검정통계량과 기각역을 구할 때, 왼쪽 기각역을 구할 경우 자유도가 바뀌며 추가적으로 F에 역수를 취해줘야한다.
ex) 동일한 회사의 공장 a, b에서 생산하는 제품의 생산량의 분산은 같거나 a가 더 작은 것으로 알려져 있는데, a 공장의 생산량의 분산이 클 수 있다는 의견이 나오고 있어 실제로 어떠한지를 알아보기 위해 각각 표본 6개와 12개를 뽑은 결과 표본분산이 각각 30과 8이 나왔다. a 공장의 생산량의 분산이 더 크다고 할 수 있는지 유의수준 10%에서 검정하시오.
a 공장의 분산이 더 크다는 것을 밝히고 싶기 때문에 이것을 대립가설로 설정한다.

검정통계량은 3.75가 나왔다.

F분포표를 통해 임계값을 구한 결과2.45가 나왔고, 검정통계량이 기각역에 위치하기에 귀무가설이 기각된다. 따라서 "a공장의 생산량 분산이 작거나 같다고 할 수 없다"
### 모비율의 차이의 추정과 가설 검정
from scipy.stats import f
import numpy as np
test_a = 0.1 #유의수준
p = 0 # 귀무가설의 모비율 차이
n1 = 6 #표본개수1
n2 = 12 #표본개수2
df1 = n1-1 #자유도1
df2 = n2-1 #자유도2
s1 = 30 #표본분산1
s2 = 8 #표본분산2
fstat = s1/s2
# 단측 검정에 따른 유의확률과 임계값
sp = 1-f.cdf(fstat, df1, df2) #유의확률
cv = f.ppf(1-test_a, df1, df2) #유의수준
print("[검정]")
print(f"임계값 : {cv:.3f}, 검정통계량 : {fstat:.2f}")
if fstat>cv:
print('귀무가설을 기각할 수 없음 = a의 분산이 더 작거나 같지 않다고 할 수 없음')
else:
print('귀무가설을 기각하고, 대립가설을 채택함 = a의 분산이 더 크다고 할 수 있음')
'Statistics' 카테고리의 다른 글
| 분산분석(ANOVA) (0) | 2024.01.23 |
|---|---|
| 분산분석(ANOVA)의 가정(feat.Python) (2) | 2024.01.18 |
| 일표본(One-sample) 검정(feat.Python) (0) | 2024.01.16 |
| 추정과 가설 검정 간단 정리 (0) | 2024.01.15 |
| F-분포(F-distribution) (1) | 2024.01.12 |



