이원분산분석은 집단의 평균에 영향을 주는 요인이 2개인 경우에 사용한다. 또한 반복이 없는 경우와 반복이 있는 경우로 나뉘는데, 샘플 수가 1개면 반복이 없는 것이고, 2개 이상이면 반복이 있는 것이다.

반복이 없는 경우를 보면 A, B 두가 요인별로 샘플이 하나씩만 있는 것을 알 수 있다.
1. 반복이 없는 경우
이원분산분석은 요인이 2개이므로 가설을 세울 때 요인 별로 따로 세워야해서 2개의 가설을 세워야한다.

또한 이원분산분석의 분산분석표에는 두 번째 요인에 해당하는 값들이 추가된다. 이에 F검정통계량 값도 두 개가 나오고, 이 것으로 두 개의 가설을 검정한다. 여기서 a는 요인A에 의한 집단 수, b는 요인B에 의한 집단 수를 나타낸다.

2. 반복이 있는 경우
반복이 있는 경우는 두 요인에 의한 각 집단끼리의 '상호작용'을 봐야한다. 아래 표를 보면 A2와 B1이 만났을 때 수치가 크게 나오고, A3와 B3가 만났을 때 수치가 작게 나오는 것을 알 수 있다. 이렇게 여러 개의 표본을 추출하면 각 집단끼리 영향을 주고 받으면서 평균이 높게 혹은 낮게 나오는 경우가 생긴다.

이렇게 두 요인이 각 집단에 독립적이지 않게 동시에 평균에 영향을 주는 것을 '상호작용' 또는 '교호작용'이라고 한다. 여기서 상호작용의 제곱합은 아래와 같이 구한다.

반복이 있는 경우는 추가로 상호작용이 있는지도 파악해야 함에 따라 가설을 3개 세워야 한다.

이에 따라 분산분석표에도 상호작용에 관한 값들이 추가된다.

EX)
1. 소를 사육하는 농가에서 4가지 종류의 사료와 3가지 종류의 사육환경에 따라 송아지의 체중이 어떻게 증가하는지 조사한 결과 아래와 같이 나왔다. 사료와 사육환경에 따라서 송아지의 체중 증가량에 차이가 있는지 유의수즌 5%에서 검정하라.

먼저 첫 번째 요인에 의한 귀무가설은 "사료에 따라 송아지 체중 증가량의 평균은 같다"이고, 두 번째 요인에 의한 귀무가설은 "사육환경에 따라 송아지 체중 증가량 평균은 같다"로 설정한다.

표본을 통해 구한 분산분석표의 값은 다음과 같다.
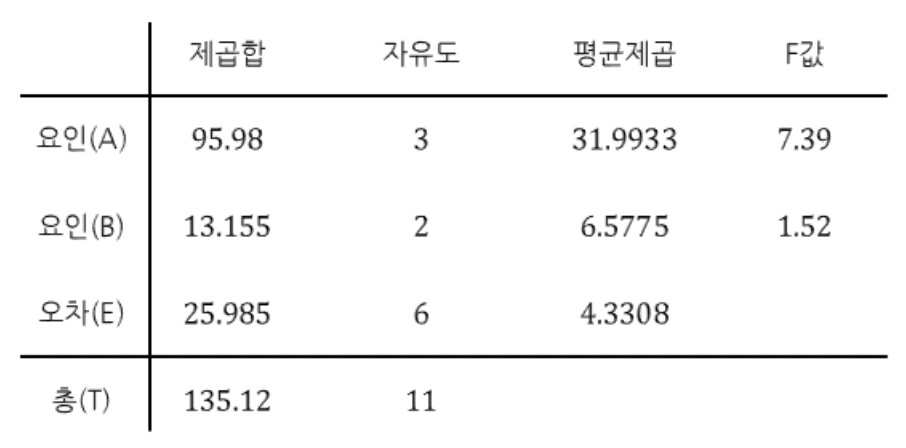
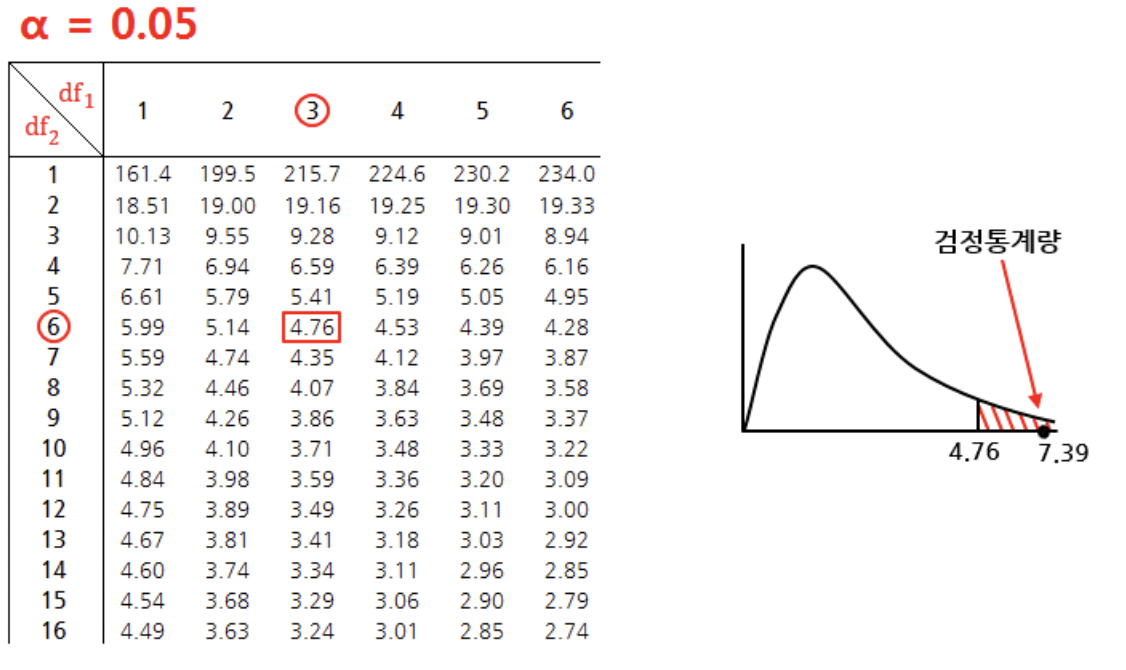
요인A에 대한 검정을 진행하면, 유의수준 0.05에서 자유도(3, 6)일 때 기각역이 4.76이고 이 때 F검정통계량은 7.39이다. 따라서 F검정통계량이 기각역 내에 위치하므로 귀무가설을 기각하고, "사료의 종류에 따라서 송아지의 체중 증가량의 평균은 같다고 할 수 없다."
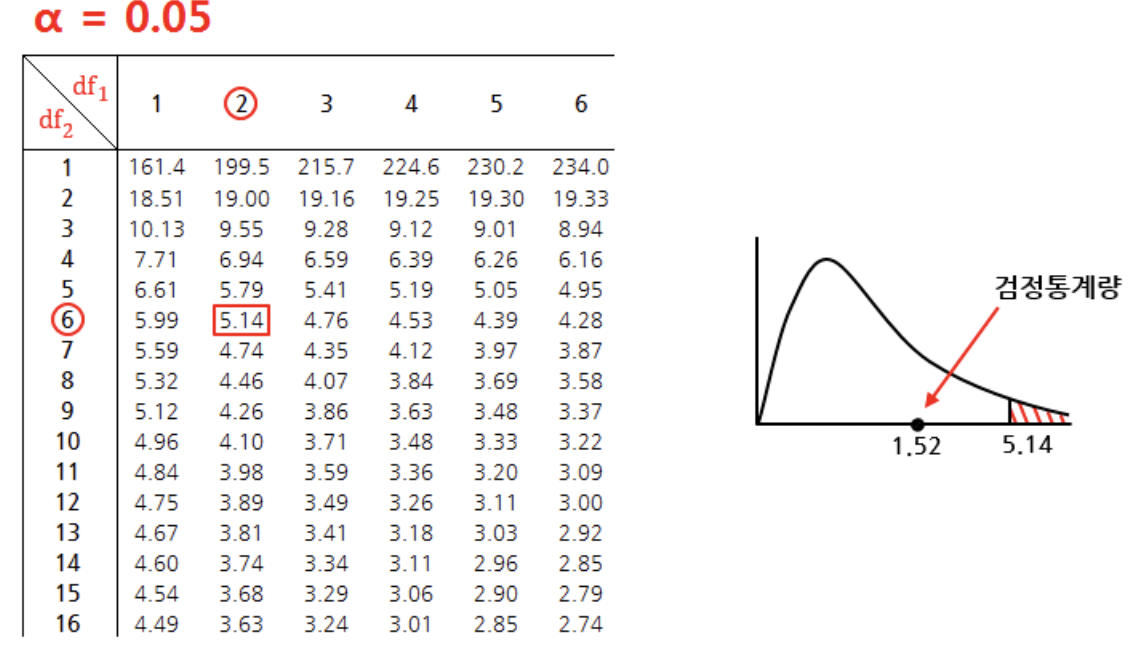
요인B에 대한 검정을 진행하면, 유의수준 0.05에서 자유도(2, 6)일 때 기각역이 5.14이고 이 때 F검정통계량은 1.52이다. 따라서 F검정통계량이 채택역 내에 위치하므로 귀무가설을 기각할 수 없고, "사육환경의 종류에 따라서 송아지의 체중 증가량의 평균은 같지 않다고 할 수 없다."
## 이원분산분석(Two-way ANOVA)
## 반복이 없는 경우(집단 별 표본 개수 1개)
from scipy.stats import f
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
import pandas as pd
import numpy as np
data = pd.DataFrame({'B1' : [54.2, 46.3, 55.3, 56.1],
'B2' : [50.7, 49.5, 49.4, 53.9],
'B3' : [49.8, 45.7, 51.9, 55.2]})
data.index = ['A1', 'A2', 'A3', 'A4']
test_a = 0.05
n = len(data.values) # 전체 표본 개수
a = data.shape[0] # A요인의 집단 개수
b = data.shape[1] # B요인의 집단 개수
dfa = a-1
dfb = b-1
dfe = dfa*dfb
mean = np.mean(data.values) # 전체 평균
a_mean = np.array(data.mean(axis=1).values) # 요인A 별 평균
b_mean = np.array(data.mean(axis=0).values) # 요인B 별 평균
SST = sum(sum((data.values - mean)**2))
SSA = sum((a_mean - mean)**2)* b
SSB = sum((b_mean - mean)**2)* a
SSE = SST-SSA-SSB # 오차 제곱합
MSA = SSA/dfa
MSB = SSB/dfb
MSE = SSE/dfe
Fa = MSA/MSE
Fb = MSB/MSE
PVa = 1-f.cdf(Fa, dfa, dfe)
PVb = 1-f.cdf(Fb, dfb, dfe)
CVa = f.ppf(1-test_a, dfa, dfe)
CVb = f.ppf(1-test_a, dfb, dfe)
table = pd.DataFrame({'요인' : ['사료(A)', '사육환경(B)', 'E'],
'자유도' : [dfa, dfb, dfe],
'SS' : [SSA, SSB, SSE],
'MS' : [MSA, MSB, MSE],
'F' : [Fa, Fb, '-'],
'PV' : [PVa, PVb, '-'],
'CV' : [CVa, CVb, '-']})
print('[요인 A F검정(오른쪽 검정)]')
if Fa > CVa:
print('귀무가설을 기각함 = 사료의 종류에 따라 송아지 체중 증가량 평균은 같다고 할 수 없다.')
else:
print('귀무가설을 기각할 수 없음 = 사료의 종류에 따라 송아지 체중 증가량 평균은 같지 않다고 할 수 없다.')
print('\n')
print('[요인 B F검정(오른쪽 검정)]')
if Fb > CVb:
print('귀무가설을 기각함 = 사육환경의 종류에 따라 송아지 체중 증가량 평균은 같다고 할 수 없다.')
else:
print('귀무가설을 기각할 수 없음 = 사육환경의 종류에 따라 송아지 체중 증가량 평균은 같지 않다고 할 수 없다.')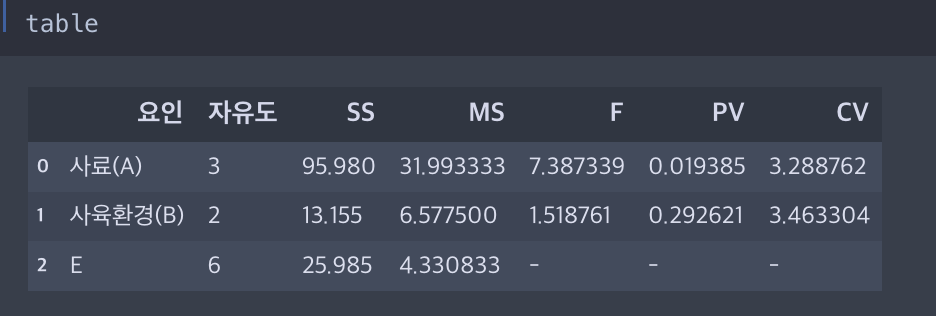

2. 어느 공장에서 4대의 기계와 3명의 작업자에 따라 제품 생산량에 차이가 있는지 파악하려한다. 실험 결과 다음과 같은 값들이 나왔을 때 기계와 작업자에 따라 제품의 생산량에 차이가 있는지 유의수준 5%에서 검정하라.
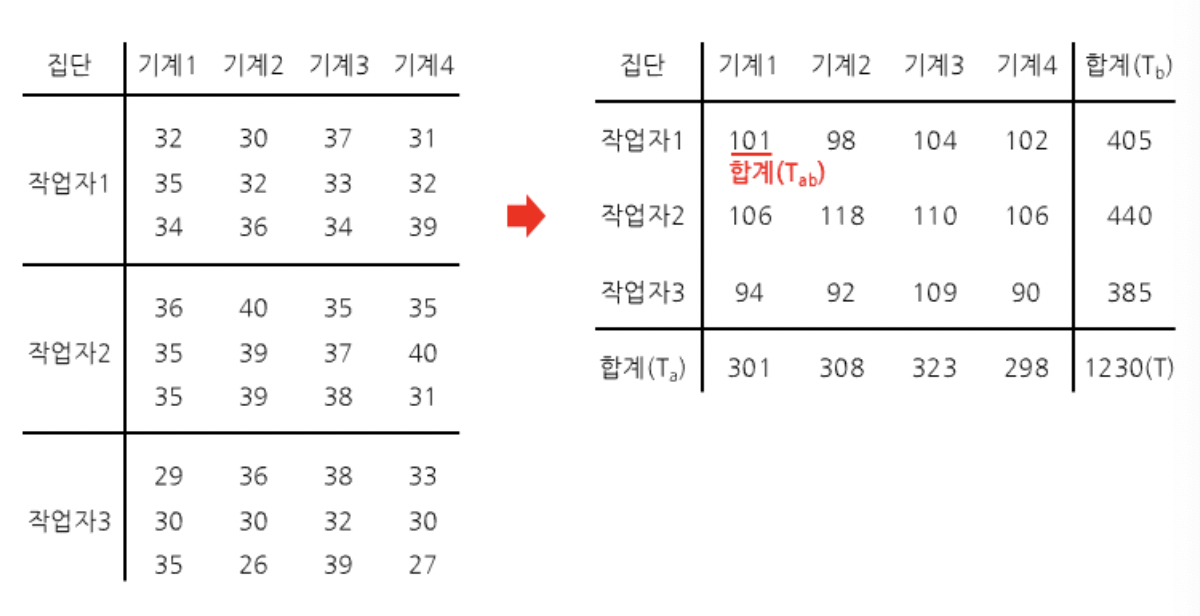
반복이 없는 경우와 마찬가지로 귀무가설을 세우면, 기계 요인에 대한 귀무가설은 "기계에 따라 생산량의 차이가 없다"이고 작업자 요인에 대한 귀무가설은 "작업자에 따라 생산량의 차이가 없다"이다. 이 후 상호작용에 대한 귀무가설을 세우면 "기계와 작업자 요인 사이에 상호작용이 없다"이고 대립가설은 "기계와 작업자 요인 사이에 상호작용이 있다"로 세운다.

표본의 값들로 분산분석표의 값들을 구하면 아래와 같다.
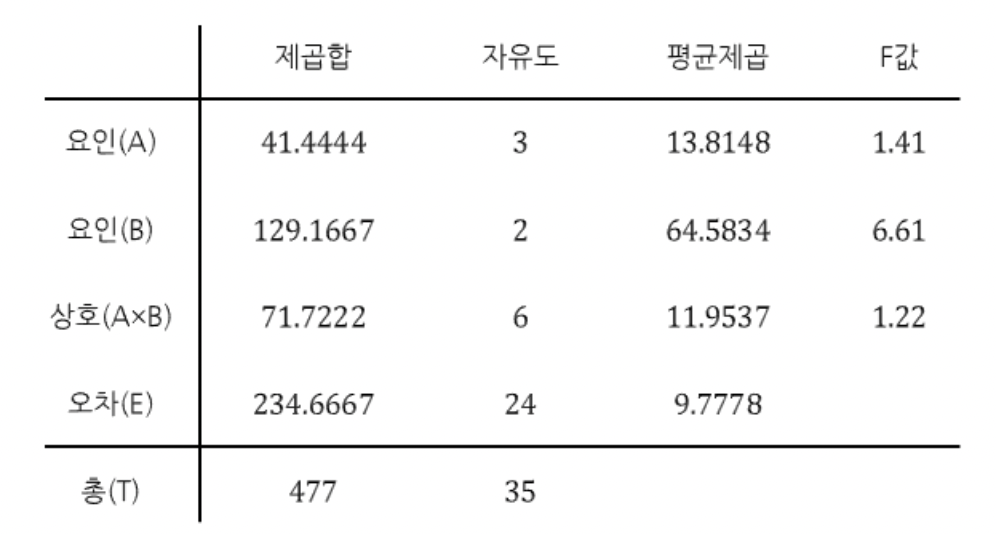
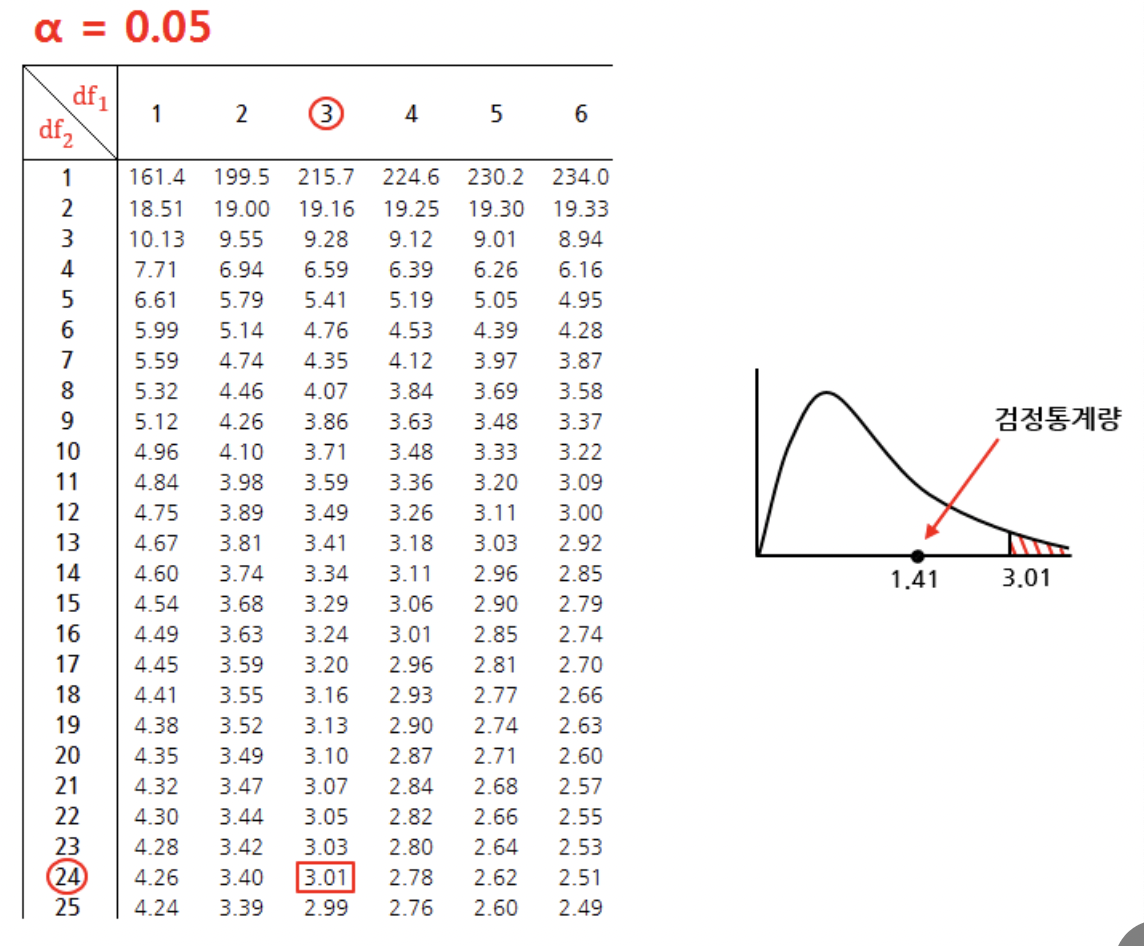
A요인인 기계 요인에 대한 검정을 진행하면, 유의수준 0.05에서 자유도(3, 24)일 F겁정통계량은 1.41, 기각역은 3.01이 나와 검정통계량이 채택역 안에 위치해 귀무가설을 기각할 수 없고, "기계에 따라 제품 생산량에 차이가 있다고 할 수 없다"
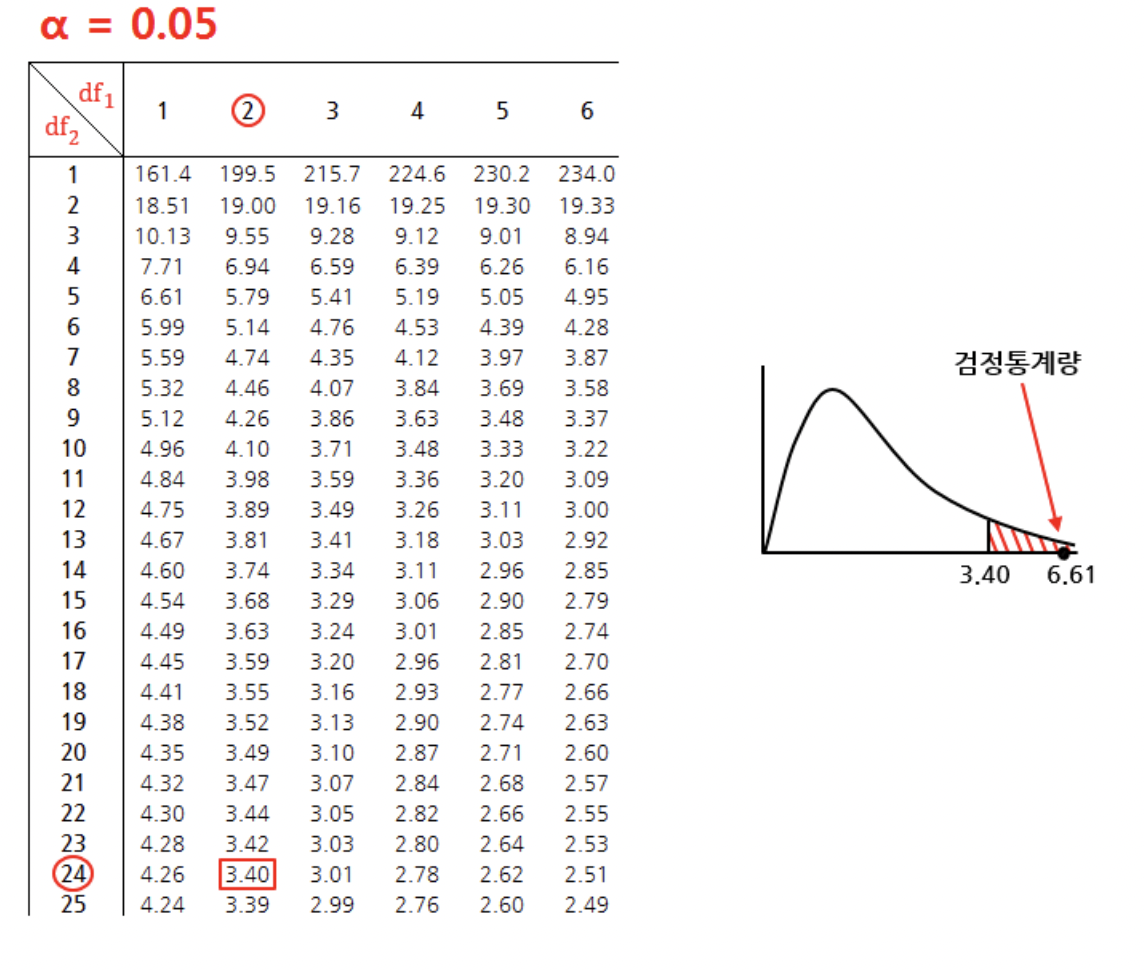
B요인인 생산자 요인에 대한 검정을 진행하면, 유의수준 0.05에서 자유도(2, 24)일 F검정통계량은 6.61, 기각역은 3.40이 나와 검정통계량이 기각역 안에 위치해 귀무가설을 기각하고, "생산자에 따라 제품 생산량에 차이가 없다고 할 수 없다"
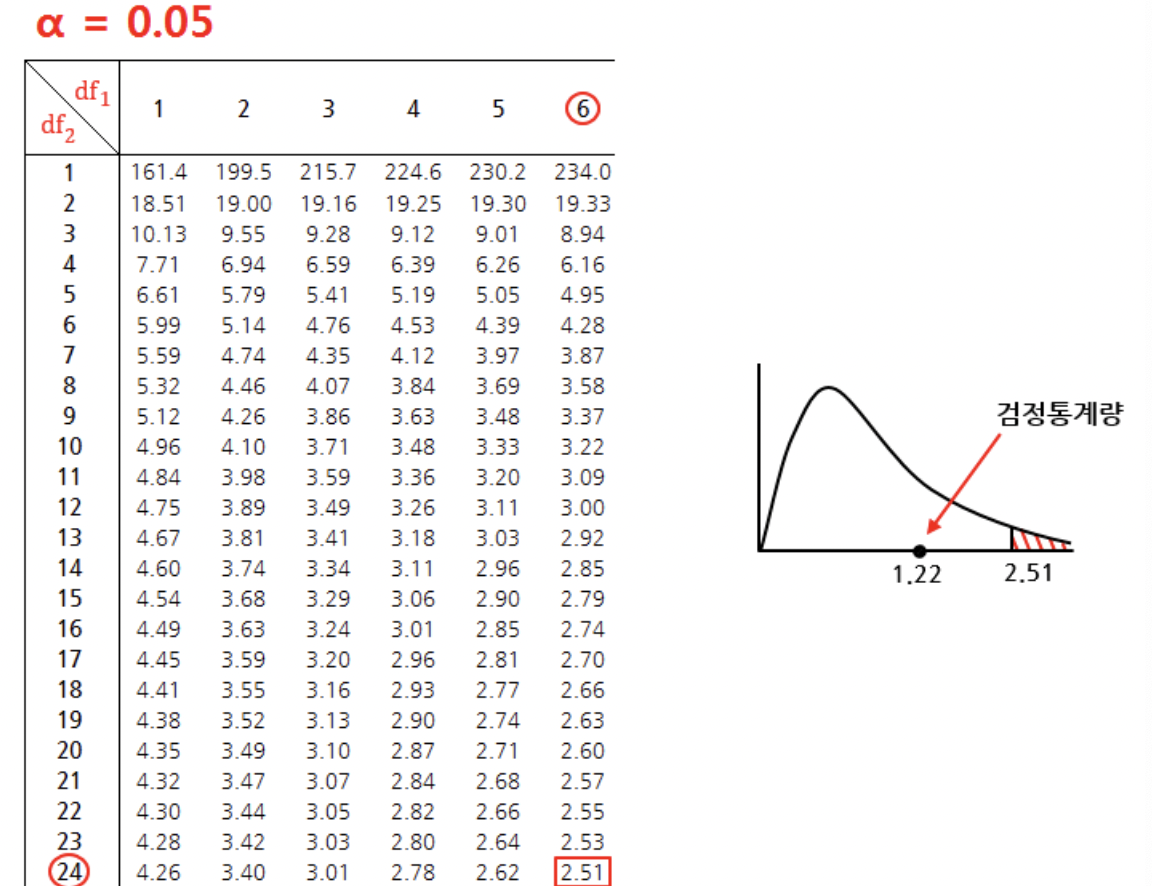
두 요인의 상호작용에 대한 검정을 진행하면, 유의수준 0.05에서 자유도가(6, 24)일 때, F검정통계량은 1.22, 기각역은 2.51이 나와 검정통계량이 채택역에 위치하므로 귀무가설을 기각할 수 없고, "두 요인에 상호작용이 있다고 할 수 없다."
## 이원분산분석(Two-way ANOVA)
## 반복이 있는 경우(집단 별 표본 개수 2개 이상)
from scipy.stats import f
import pandas as pd
import numpy as np
A1 = pd.DataFrame({'B1' : [32, 35, 34],
'B2' : [36, 35, 35],
'B3' : [29, 30, 35]})
A2 = pd.DataFrame({'B1' : [30, 32, 36],
'B2' : [40, 39, 39],
'B3' : [36, 30, 26]})
A3 = pd.DataFrame({'B1' : [37, 33, 34],
'B2' : [35, 37, 38],
'B3' : [38, 32, 39]})
A4 = pd.DataFrame({'B1' : [31, 32, 39],
'B2' : [35, 40, 31],
'B3' : [33, 30, 27]})
data = [A1, A2, A3, A4]
test_a = 0.05
n = np.sum([len(df.values.flatten()) for df in data]) # 전체 표본 개수
a = len(data) # A요인의 집단 개수
b = len(data[0].columns)# B요인의 집단 개수
r = len(data[0].index) # 반복 횟수
dfa = a-1
dfb = b-1
dfab = dfa*dfb
dfe = a*b*(r-1)
mean = np.sum([df.sum().sum() for df in data]) / n # 전체 평균
a_mean = np.array([df.mean().mean() for df in data]) # 요인A 별 평균
b_mean = [] # 요인B 별 평균
for b_ in ['B1', 'B2', 'B3']:
b_mean_ = 0
for df in data:
b_mean_ += df[b_].mean()
b_mean.append(b_mean_/4)
ab_mean = []
for df in data:
for b_ in ['B1', 'B2', 'B3']:
ab_mean.append(df[b_].mean())
SST = sum(sum((data[0].values - mean)**2)
+ sum((data[1].values - mean)**2)
+sum((data[2].values - mean)**2)
+ sum((data[3].values - mean)**2))
SSA = sum((a_mean - mean)**2) * b * r
SSB = sum((b_mean - mean)**2) * a * r
SSAB = 0 # 상호작용 제곱합
cnt = 0
for aidx, df in enumerate(data):
for bidx, b_ in enumerate(['B1', 'B2', 'B3']):
SSAB += (ab_mean[cnt]-a_mean[aidx]-b_mean[bidx]+mean)**2
cnt += 1
SSAB *= r
SSE = SST-SSA-SSB-SSAB
MSA = SSA/dfa
MSB = SSB/dfb
MSAB = SSAB/dfab
MSE = SSE/dfe
Fa = MSA/MSE
Fb = MSB/MSE
Fab = MSAB/MSE
PVa = 1-f.cdf(Fa, dfa, dfe)
PVb = 1-f.cdf(Fb, dfb, dfe)
PVab = 1-f.cdf(Fab, dfab, dfe)
CVa = f.ppf(1-test_a, dfa, dfe)
CVb = f.ppf(1-test_a, dfb, dfe)
CVab = f.ppf(1-test_a, dfab, dfe)
table = pd.DataFrame({'요인' : ['기계(A)', '작업자(B)', 'AxB', 'E'],
'자유도' : [dfa, dfb,dfab, dfe],
'SS' : [SSA, SSB, SSAB, SSE],
'MS' : [MSA, MSB, MSAB, MSE],
'F' : [Fa, Fb, Fab, '-'],
'PV' : [PVa, PVb, PVab, '-'],
'CV' : [CVa, CVb, CVab, '-']})
print('[요인 A F검정(오른쪽 검정)]')
if Fa > CVa:
print('귀무가설을 기각함 = 기계의 종류에 따라 제품 생산량 평균은 같다고 할 수 없다.')
else:
print('귀무가설을 기각할 수 없음 = 기계의 종류에 따라 제품 생산량 평균은 같지 않다고 할 수 없다.')
print('\n')
print('[요인 B F검정(오른쪽 검정)]')
if Fb > CVb:
print('귀무가설을 기각함 = 생산자에 따라 제품 생산량 평균은 같다고 할 수 없다.')
else:
print('귀무가설을 기각할 수 없음 = 생산자에 따라 제품 생산량 평균은 같지 않다고 할 수 없다.')
print('\n')
print('상호작용 검정')
if Fab > CVab:
print('귀무가설을 기각함 = 두 요인 사이에 상호작용이 없다고 할 수 없다.')
else:
print('귀무가설을 기각할 수 없음 = 두 요인 사이에 상호작용이 있다고 할 수 없다.')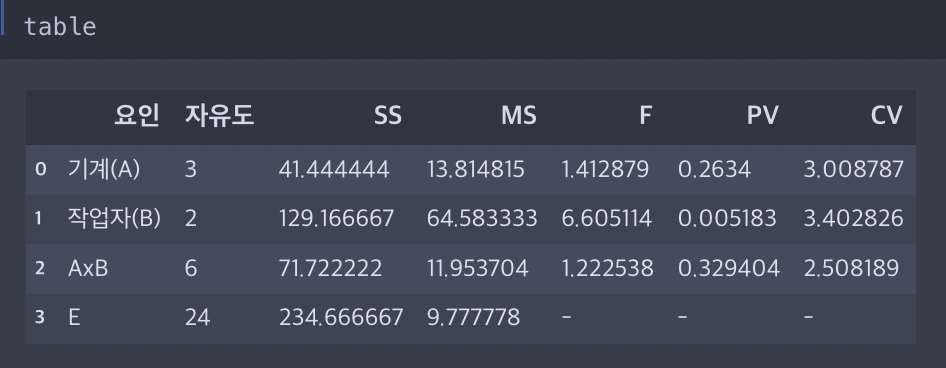

'Statistics' 카테고리의 다른 글
| 일원분산분석 (One-way ANOVA)(feat. Python) (0) | 2024.01.23 |
|---|---|
| 분산분석(ANOVA) (0) | 2024.01.23 |
| 분산분석(ANOVA)의 가정(feat.Python) (1) | 2024.01.18 |
| 이표본 검정(Two-sample)(feat.Python) (1) | 2024.01.17 |
| 일표본(One-sample) 검정(feat.Python) (0) | 2024.01.16 |



